题目内容
集合S={0,1,2,3,4,5},A是S的子集.当x∈A时,有(x-1)∈A且(x+1)∈A,则称x为A的一个“连续元素”.那么S的所有子集中,只含有两个“连续元素”的子集的个数为( )
| A、3个 | B、4个 | C、5个 | D、6个 |
考点:集合的包含关系判断及应用
专题:集合
分析:由A⊆S,结合x∈A时,有x-1∈A,且x+1∈A,则称x为A的一个“连续元素”,用列举法列出满足条件的所有集合,得到答案.
解答:
解:∵S={0,1,2,3,4,5},A⊆S,
∴A中只含有两个“连续元素”的集合是:
{0,1,2,3},{1,2,3,4},{2,3,4,5},{0,1,2,3,5},{0,2,3,4,5}共5个
∴S中满足条件的子集A的个数是5个.
故选:C.
∴A中只含有两个“连续元素”的集合是:
{0,1,2,3},{1,2,3,4},{2,3,4,5},{0,1,2,3,5},{0,2,3,4,5}共5个
∴S中满足条件的子集A的个数是5个.
故选:C.
点评:本题考查了元素与集合关系的判断问题,解题时要根据题意列出满足条件的集合,以便得出正确答案.

练习册系列答案
相关题目
已知实数x、y满足
,则|x+2y-6|-3y的最大值是( )
|
| A、0 | B、2 | C、4 | D、-4.8 |
已知A(-2,0),B(2,0),点P在圆(x-3)2+(y-4)2=4上运动,则|PA|2+|PB|2的最小值是( )
| A、22 | B、10 | C、36 | D、26 |
已知曲线y=2x3上一点A(1,2),则A处切线的斜率是( )
| A、2 | B、3 | C、4 | D、6 |
若双曲线
-
=1的离心率为2,则实数m的值为( )
| x2 |
| 2 |
| y2 |
| m |
A、2
| ||
| B、3 | ||
C、
| ||
| D、6 |
已知集合A={x|-2≤x≤3},B={x|-1≤x≤4},那么集合A∩B等于( )
| A、{x|-2≤x≤4} |
| B、{x|3≤x≤4} |
| C、{x|-2≤x≤-1} |
| D、{x|-1≤x≤3} |
抛物线y2=20x的焦点坐标为( )
| A、(10,0) |
| B、(5,0) |
| C、(0,10) |
| D、(0,5) |
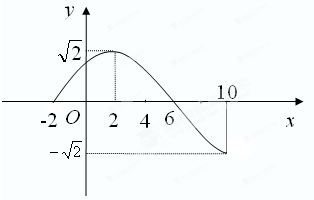 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<