题目内容
1.己知A(-1,4),B(3,-2),以AB为直径的圆交直线y=x+1于M、N两点,则|MN|=5$\sqrt{2}$.分析 求出以AB为直径的圆的方程,圆心到直线的距离,即可得出结论.
解答 解:A(-1,4),B(3,-2),以AB为直径的圆的方程为(x-1)2+(y-1)2=13
圆心到直线的距离d=$\frac{1}{\sqrt{2}}$,
∴|MN|=2$\sqrt{13-\frac{1}{2}}$=5$\sqrt{2}$.
故答案为:5$\sqrt{2}$.
点评 本题考查圆的方程,考查学生的计算能力,比较基础.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
9.已知$\overrightarrow{a}$=(1,-2,1),$\overrightarrow{a}$+$\overrightarrow{b}$=(-1,2,-1),则$\overrightarrow{b}$等于( )
| A. | (2,-4,2) | B. | (-2,4,-2) | C. | (-2,0,-2) | D. | (2,1,-3) |
13.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2|$\overrightarrow{b}$|≠0,且关于x的函数f(x)=2x3-3|$\overrightarrow{a}$|x2+6$\overrightarrow{a}$•$\overrightarrow{b}$x+5在实数集R上有极值,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角的取值范围是( )
| A. | ($\frac{π}{3}$,π) | B. | ($\frac{π}{3}$,π] | C. | [$\frac{π}{3}$,π] | D. | (0,$\frac{π}{3}$) |
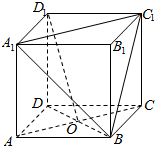 已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.