题目内容
已知曲线C：x2+y2+Gx+Ey+F=0（G2+E2-4F＞0），求曲线C在x轴上的所截的线段的长度为1的充要条件，证明你的结论．
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据圆的一般方程，结合充分条件和必要条件的定义进行证明即可．
解答：
解：必要性：令y=0，则x2+Gx+F=0.设x1 、x2为此方程的根，若|x1-x2|=
=1，则G2-4F=1．
充分性：若G2-4F=1，则x2+Gx+F=0．
有两根为x1、x2，且x1+x2=-G，x1•x2=F，|x1-x2|2=(x1+x2)2-4x1•x2=G2-4F=1．
故所求的充要条件是G2-4F=1．
| G2-4F |
充分性：若G2-4F=1，则x2+Gx+F=0．
有两根为x1、x2，且x1+x2=-G，x1•x2=F，|x1-x2|2=(x1+x2)2-4x1•x2=G2-4F=1．
故所求的充要条件是G2-4F=1．
点评：本题主要考查充分条件和必要条件的应用，根据圆的一般方程以及充分条件和必要条件的定义是解决本题的关键．
练习册系列答案
阳光课堂课时作业系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
下列两个变量之间的关系哪个不是函数关系（ ）
| A、人的年龄和身高 |
| B、正方形的边长和面积 |
| C、正n边形的边数与顶点角度之和 |
| D、角度与它的余弦值 |
下列函数中，是奇函数的是（ ）
| A、y=x2+x |
| B、y=x2+1 |
| C、y=x3+x |
| D、y=x2+x3 |
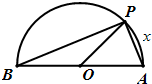如图，点P在半径为1的半圆上运动，AB是直径，当P沿半圆弧从A到B运动时，点P经过的路程x与△APB的面积y的函数y=f（x）的图象是下图中的（ ）
