题目内容
已知关于x的方程sin2x+cosx+a=0有解,则a的取值范围是( )
| A、[-1,1] | ||
B、[-1,
| ||
C、[-
| ||
D、[-
|
考点:二次函数在闭区间上的最值,正弦函数的定义域和值域
专题:函数的性质及应用
分析:利用参数分离法,将方程进行分离,利用二次函数的图象和性质即可得到结论.
解答:
解:∵sin2x+cosx+a=0,
∴a=-sin2x-cosx=cos2x-1-cosx=(cosx-
)2-
,
∵-1≤cosx≤1,
∴-
≤(cosx-
)2-
≤1,
若方程有解,则-
≤a≤1,
故选:C
∴a=-sin2x-cosx=cos2x-1-cosx=(cosx-
| 1 |
| 2 |
| 5 |
| 4 |
∵-1≤cosx≤1,
∴-
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
若方程有解,则-
| 5 |
| 4 |
故选:C
点评:本题主要考查三角函数图象和性质,利用二次函数的图象和性质即可得到结论.

练习册系列答案
相关题目
在复平面内,复数
对应的点位于( )
| 1-2i |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
当x>0,y>0,
+
=1时,x+y的最小值为( )
| 1 |
| x |
| 9 |
| y |
| A、10 | B、12 | C、14 | D、16 |
已知数列{an}首项为1,且满足an+1=
an,那么an等于( )
| n+1 |
| n |
| A、n | ||
| B、n+1 | ||
C、
| ||
D、
|
已知
+
>1+2m(x>0,y>0)恒成立,则实数m的取值范围是( )
| 2y |
| x |
| 8x |
| y |
A、m>
| ||
B、m<
| ||
| C、m<2 | ||
| D、m>2 |
等差数列{an}中a1>0,S5=S8,则当Sn取最大值时n的值是( )
| A、6 | B、7 | C、6或7 | D、不存在 |
下面是一个2×2列联表,则a-b的值等于( )
| y1 | y2 | 总计 | |
| x1 | c | a | 69 |
| x2 | b | d | f |
| 总计 | e | 65 | 99 |
| A、45 | B、35 | C、34 | D、25 |
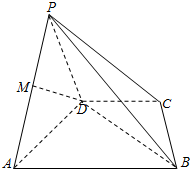 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.