题目内容
18.在直角坐标系中,如果不同的两点A(a,b),B(-a,-b)都在函数y=f(x)的图象上,那么称[A,B]为函数f(x)的一组关于原点的中心对称点([A,B]与[B,A]看作同一组),函数g(x)=$\left\{\begin{array}{l}{sin\frac{π}{2}x,x≤0}\\{lo{g}_{2}(x+1),x>0}\end{array}\right.$,关于原点的中心对称点的组数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 利用定义,只要求出g(x)=sin$\frac{π}{2}x$,x≤0,关于原点对称的函数h(x)=sin$\frac{π}{2}x$,x>0,观察h(x)与g(x)=log2(x+1),x>0的交点个数,即为中心对称点的组数.
解答  解:由题意可知g(x)=sin$\frac{π}{2}x$,x≤0,则函数g(x)=sin$\frac{π}{2}x$,x≤0,
解:由题意可知g(x)=sin$\frac{π}{2}x$,x≤0,则函数g(x)=sin$\frac{π}{2}x$,x≤0,
关于原点对称的函数为h(x)=sin$\frac{π}{2}x$,x>0,
则坐标系中分别作出函数h(x)=sin$\frac{π}{2}x$,x>0,g(x)=log2(x+1),x>0的图象如图,
由图象可知,两个图象的交点个数有1个,
所以函数g(x)=$\left\{\begin{array}{l}{sin\frac{π}{2}x,x≤0}\\{lo{g}_{2}(x+1),x>0}\end{array}\right.$关于原点的中心对称点的组数为1组.
故选:B
点评 本题主要考查函数的交点问题,利用定义先求出函数关于原点对称的函数,是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
8.在数列{an}中,a7=16,an-$\frac{1}{2}$an+1=0,则a2的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
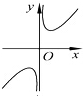
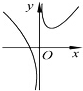
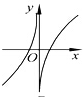
9.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是( )
| A. | y=x3 | B. | y=|x+1| | C. | y=-x2 | D. | y=|x|+1 |
6.用边长为120cm的正方形铁皮做一个无盖水箱,先在四周分别截去一个小正方形,然后把四边翻转90°角,再焊接成水箱,则水箱的最大容积为( )
| A. | 120 000 cm3 | B. | 128 000 cm3 | C. | 150 000 cm3 | D. | 158 000 cm3 |
3.随机抛掷一枚质地均匀的骰子,记正面向上的点数为a,则函数f(x)=x2+2ax+2有两个不同零点的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
8.执行如图所示的程序框图,若要使输出的y的值等于3,则输入的x的值可以是( )
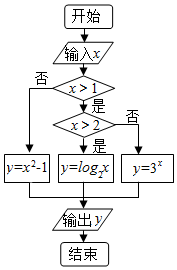

| A. | 1 | B. | 2 | C. | 8 | D. | 9 |

 如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).
如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).