题目内容

13．已知函数$f（x）=x+\frac{1}{x}$，则函数y=f（x）的大致图象为（　　）
A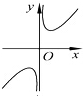．B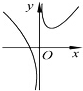．C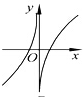．D．

分析 利用函数的定义域和函数奇偶性以及函数的零点即可判断．

解答 解：f（x）的定义域为（-∞，0）∪（0，+∞），
f（-x）=-f（x），即函数f（x）为奇函数，排除，B，D，
令f（x）=0，即x+$\frac{1}{x}$=0，得$\frac{{x}^{2}+1}{x}$=0，则方程无解，即函数f（x）无零点，排除C
故选：A．

点评 本题考查了函数图象的识别，关键是判断函数的奇偶性和函数的零点，属于基础题．

练习册系列答案
相关题目
3．在△ABC中，角A，B，C的对边分别为a，b，c，若a2=b2+$\frac{1}{4}{c^2}$，则$\frac{acosB}{c}$=$\frac{5}{8}$．
4．执行如图所示的程序框图，若输出s=15，则框图中①处可以填入k＜4．
1．在下列函数中既是奇函数，又是在区间（0，+∞）上单调递减的函数为（　　）
A．$y=ln\frac{1}{|x|}$B．y=x-1C．$y={（{\frac{1}{2}}）^x}$D．y=x3+x
8．若三棱锥的一条棱长为x，其余棱长均为1，则该三棱锥的体积（　　）
A．有最大值无最小值B．有最小值无最大值
C．既有最大值又有最小值D．既无最大值也无最小值
18．在直角坐标系中，如果不同的两点A（a，b），B（-a，-b）都在函数y=f（x）的图象上，那么称[A，B]为函数f（x）的一组关于原点的中心对称点（[A，B]与[B，A]看作同一组），函数g（x）=$\left\{\begin{array}{l}{sin\frac{π}{2}x，x≤0}\\{lo{g}_{2}（x+1），x＞0}\end{array}\right.$，关于原点的中心对称点的组数为（　　）
A．0B．1C．2D．3
5．已知函数$f（x）=\frac{lnx}{x}$．
（Ⅰ）记函数$F（x）={x^2}-x•f（x）（{x∈[{\frac{1}{2}，2}]}）$，求函数F（x）的最大值；
（Ⅱ）记函数$H（x）=\left\{\begin{array}{l}\frac{x}{2e}，x≥s\\ f（x），0＜x＜s\end{array}\right.$若对任意实数k，总存在实数x0，使得H（x0）=k成立，求实数s的取值集合．
2．已知f（x）=m（x-m）（x+m+3）在区间[1，+∞）上的值恒为负数，且在区间（-∞，-4）上存在x0使得f（x0）＞0，求实数m的取值范围．
3．已知{an}是等差数列，{bn}是各项均为正数的等比数列，若a1=b1=1，a1+a2+a3=a5，b1+b2+b3=a4，则a5+b5=（　　）
A．10B．15C．20D．25

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网