题目内容
6．设$\overrightarrow{a}$、$\overrightarrow{b}$是两个不平行的非零向量，且x（2$\overrightarrow{a}$+$\overrightarrow{b}$）+y（3$\overrightarrow{a}$-2$\overrightarrow{b}$）=7$\overrightarrow{a}$，x、y∈R，求实数x、y的值．分析 利用向量相等列出方程组求解即可．
解答 解：$\overrightarrow{a}$、$\overrightarrow{b}$是两个不平行的非零向量，且x（2$\overrightarrow{a}$+$\overrightarrow{b}$）+y（3$\overrightarrow{a}$-2$\overrightarrow{b}$）=7$\overrightarrow{a}$，x、y∈R，
可得$\left\{\begin{array}{l}{2x+3y=9}\\{x-2y=0}\end{array}\right.$，
解得x=$\frac{18}{7}$，y=$\frac{9}{7}$．
点评 本题考查向量相等的充要条件的应用，考查计算能力．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
14．已知P（x，y）是中心在原点，焦距为4$\sqrt{2}$的双曲线上一点，且$\frac{y}{x}$的取值范围为（-1，1），则该双曲线的方程是（ ）
| A． | x2-y2=8 | B． | y2-x2=8 | C． | x2-y2=4 | D． | y2-x2=4 |
1．点M（π，-m）在函数y=cosx-1的图象上，则m的值为（ ）
| A． | -2 | B． | 0 | C． | 1 | D． | 2 |
11．
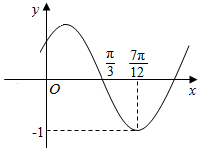函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，将函数f（x）的图象向右平移$\frac{π}{6}$个单位后得到的函数图象的解析式为（ ）
函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，将函数f（x）的图象向右平移$\frac{π}{6}$个单位后得到的函数图象的解析式为（ ）| A． | y=sin2x | B． | y=sin（2x+$\frac{π}{3}$） | C． | y=sin（2x+$\frac{π}{6}$） | D． | y=sin（2x-$\frac{π}{3}$） |