题目内容
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.
(1) 若c=2,C=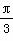 ,且△ABC的面积为
,且△ABC的面积为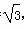 ,求a、b的值;
,求a、b的值;
(2) 若sinC+sin(B-A)=sin2A,试判断△ABC的形状.
解:(1) ∵ c=2,C=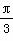 ,∴ 由余弦定理c2=a2+b2-2abcosC,得a2+b2-ab=4.又△ABC的面积为
,∴ 由余弦定理c2=a2+b2-2abcosC,得a2+b2-ab=4.又△ABC的面积为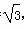 ,
,
∴ 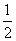 absinC=
absinC=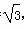 ,即ab=4.联立方程组
,即ab=4.联立方程组
解得a=2,b=2.
(2) 由sinC+sin(B-A)=sin2A,得sin(A+B)+sin(B-A)=2sinAcosA,即2sinBcosA=2sinAcosA,∴ cosA·(sinA-sinB)=0,∴ cosA=0或sinA-sinB=0.当cosA=0时,∵ 0<A<π,∴ A=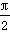 ,△ABC为直角三角形;当sinA-sinB=0时,得sinB=sinA,由正弦定理得a=b,即△ABC为等腰三角形.∴ △ABC为等腰三角形或直角三角形.
,△ABC为直角三角形;当sinA-sinB=0时,得sinB=sinA,由正弦定理得a=b,即△ABC为等腰三角形.∴ △ABC为等腰三角形或直角三角形.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 ,3
,3 ,5
,5 ,7
,7 , …
, …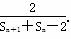 .
.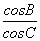 =-
=-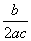 .
.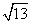 ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积. ,C=
,C= ,则△ABC的面积为________.
,则△ABC的面积为________.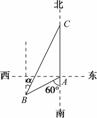
 ,求
,求 的值.
的值.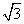 b .求角A的大小.
b .求角A的大小.