题目内容

11．若集合A={x|3+2x-x2＞0}，集合B={x|2x＜2}，则A∩B等于（　　）
A．（1，3）B．（-∞，-1）C．（-1，1）D．（-3，1）

分析 分别求出关于集合A、B中x的范围，取交集即可．

解答 解：∵集合A={x|3+2x-x2＞0}={x|-1＜x＜3}，
集合B={x|2x＜2}={x|x＜1}，
则A∩B={x|-1＜x＜1}，
故选：C．

点评 本题考察了集合的运算性质，考察解不等式问题，是一道基础题．

练习册系列答案
相关题目
19．函数y=2x（3-x）的递增区间是（-∞，$\frac{3}{2}$]．
2．若l、m、n是互不相同的空间直线，α，β是不重合的平面，则下列选项中正确的是（　　）
A．若α∥β，l?α，n?β，则l∥nB．若α⊥β，l?α，则l⊥β
C．若l⊥α，l∥β，则α⊥βD．若l⊥n，m⊥n，则l∥m
19．（1）若方程|3x-1|=k有两个不同解，求实数k的取值范围；
（2）求函数$f（x）=\left\{\begin{array}{l}{x^2}-2，\;\;\;\;\;\;\;\;\;x≤0\\ 2x-6+lnx，x＞0\end{array}\right.$的零点个数；
（3）设f（x）=x2-3x+a．若函数f（x）在区间（1，3）内有根，求实数a的取值范围．
6．设函数f（x）是定义在R上的周期为3的偶函数，当$x∈[0，\frac{3}{2}]$时，f（x）=x+1，则$f（\frac{5}{2}）$=$\frac{3}{2}$．
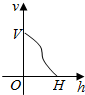
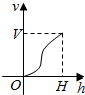
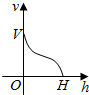
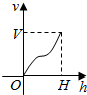
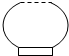16．一高为H，满缸水量为V的鱼缸截面如图所示，其底部破了一个小洞，缸中水从洞中流出，若鱼缸水深为h时水的体积为v，则函数v=f（h）的大致图象可能是图中四个选项中的（　　）
A．B．C．D．
3．将函数f（x）=2sin（2x-$\frac{π}{6}$）的图象向左平移m个单位（m＞0），若所得的图象关于直线x=$\frac{π}{6}$对称，则m的最小值为$\frac{π}{6}$．
20．已知函数f（x）=ax3+$\frac{b}{x}$+5（a，b∈R），若f（2）=3，则f（-2）=（　　）
A．7B．3C．-7D．-3
1．已知集合A={0，1}，B={2，a2}，且A∪B={0，1，2，4}，则a的值为（　　）
A．2B．-2C．4D．±2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网