题目内容

双曲线H的离心率为e,左、右焦点为F1、F2,能否在H的左支上找到点P,使|PF1|是P到左准线l1的距离d1与|PF2|的等比中项？

思路分析:本题为存在性问题,先假设点P(x,y)(x≤-a)存在,又涉及到焦半径|PF1|、|PF2|,据双曲线上点的坐标与焦半径关系应从焦半径公式入手.

解:H:=1,设点P(x,y)(x≤-a)存在,

|PF1|2=d1·|PF2|(ex+a)2

=·|ex-a|

=·(a-ex)e(ex+a)

=-(a-ex).

x=≤-ae2-2e-1≤01＜e≤1+.

故当e∈(1,1+)时,能在H的左支上找到点P,其横坐标为x=.

练习册系列答案
相关题目
已知以原点O为中心，F(
5
，0)为右焦点的双曲线C的离心率e=
5
2
．
（1）求双曲线C的标准方程及其渐近线方程；
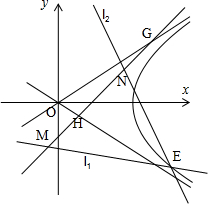
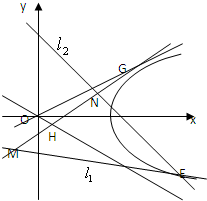
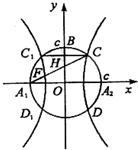（2）如图，已知过点M（x1，y1）的直线l1：x1x+4y1y=4与过点N（x2，y2）（其中x2≠x）的直线l2：x2x+4y2y=4的交点E在双曲线C上，直线MN与两条渐近线分别交与G、H两点，求△OGH的面积．精英家教网精英家教网
精英家教网如图，以A1，A2为焦点的双曲线E与半径为c的圆O相交于C，D，C1，D1，连接CC1与OB交于点H，且有：
OH
=(3+2
3
)
HB
．其中A1，A2，B是圆O与坐标轴的交点，c为双曲线的半焦距．
（1）当c=1时，求双曲线E的方程；
（2）试证：对任意正实数c，双曲线E的离心率为常数．
（3）连接A1C与双曲线E交于F，是否存在
实数λ，使
A1F
=λ
FC
恒成立，若存在，试求出λ的值；若不存在，请说明理由．
已知双曲线H：
x2
a2
-
y2
b2
=1（a＞0，b＞0）一个顶点为（2，0），且H的离心率e=
5
2
．
（1）求H的方程；
（2）过原点的直线l与H相交于A、B两点（点A在第一象限），过A作AC垂直于x轴，垂足为C．连接BC与H交于点D，记直线AB，AD的斜率分别为k1、k2．求证：k1+k2＞
3
2
．
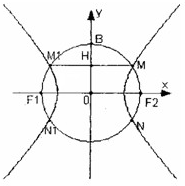如图，F1（-c，0），F2（c，0）为双曲线E的两焦点，以F1F2为直径的圆O与双曲线E交于M、N、M1、N1，B是圆O与y轴的交点，连接MM1与OB交于H，且H是OB的中点．
（1）当c=1时，求双曲线E的方程；
（2）试证：对任意的正实数c，双曲线E的离心率为常数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网