题目内容
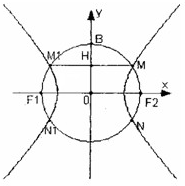 如图,F1(-c,0),F2(c,0)为双曲线E的两焦点,以F1F2为直径的圆O与双曲线E交于M、N、M1、N1,B是圆O与y轴的交点,连接MM1与OB交于H,且H是OB的中点.
如图,F1(-c,0),F2(c,0)为双曲线E的两焦点,以F1F2为直径的圆O与双曲线E交于M、N、M1、N1,B是圆O与y轴的交点,连接MM1与OB交于H,且H是OB的中点.(1)当c=1时,求双曲线E的方程;
(2)试证:对任意的正实数c,双曲线E的离心率为常数.
分析:(1)由c=1,知B(0,1),H(0,
),M(
,
),由M在E上,知
,由此能求出双曲线E的方程.
(2)由F1(-c,0),B(0,c),H(0,
),M(
,
),知3e4-8e2+4=1,由此能证明e为常数.
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
|
(2)由F1(-c,0),B(0,c),H(0,
| c |
| 2 |
| ||
| 2 |
| c |
| 2 |
解答:(1)解:∵c=1,
∴B(0,1),H(0,
),M(
,
),
设E:
-
=1(a>0,b>0),
∵M在E上,则
∴
,
解得
,
∴双曲线E的方程为:2x2-2y2=1…7分
(2)证明:F1(-c,0),B(0,c),H(0,
),M(
,
)
设E:
-
=1(a>0,b>0),
,即3e4-8e2+4=1,
解得e2=2或e2=
(舍),
∴e=
为常数. 7分.
∴B(0,1),H(0,
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
设E:
| x2 |
| a2 |
| y2 |
| b2 |
∵M在E上,则
∴
|
解得
|
∴双曲线E的方程为:2x2-2y2=1…7分
(2)证明:F1(-c,0),B(0,c),H(0,
| c |
| 2 |
| ||
| 2 |
| c |
| 2 |
设E:
| x2 |
| a2 |
| y2 |
| b2 |
|
解得e2=2或e2=
| 2 |
| 3 |
∴e=
| 2 |
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,双曲线的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
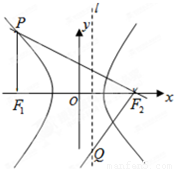
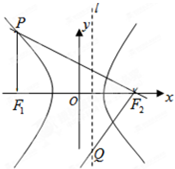 如图,F1(-c,0),F2(c,0)分别是双曲线C:
如图,F1(-c,0),F2(c,0)分别是双曲线C: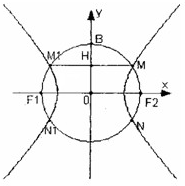 如图,F1(-c,0),F2(c,0)为双曲线E的两焦点,以F1F2为直径的圆O与双曲线E交于M、N、M1、N1,B是圆O与y轴的交点,连接MM1与OB交于H,且H是OB的中点.
如图,F1(-c,0),F2(c,0)为双曲线E的两焦点,以F1F2为直径的圆O与双曲线E交于M、N、M1、N1,B是圆O与y轴的交点,连接MM1与OB交于H,且H是OB的中点. 如图,F1(-c,0),F2(c,0)分别是双曲线C:
如图,F1(-c,0),F2(c,0)分别是双曲线C: -
- =1(a>0,b>0)的左,右焦点,过点F1作x轴的垂线交双曲线的上半部分于点P,过点F2作直线PF2的垂线交直线l:x=
=1(a>0,b>0)的左,右焦点,过点F1作x轴的垂线交双曲线的上半部分于点P,过点F2作直线PF2的垂线交直线l:x= 于点Q,若点Q的坐标为(1,-4).
于点Q,若点Q的坐标为(1,-4).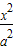 -
-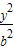 =1(a>0,b>0)的左,右焦点,过点F1作x轴的垂线交双曲线的上半部分于点P,过点F2作直线PF2的垂线交直线l:x=
=1(a>0,b>0)的左,右焦点,过点F1作x轴的垂线交双曲线的上半部分于点P,过点F2作直线PF2的垂线交直线l:x=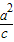 于点Q,若点Q的坐标为(1,-4).
于点Q,若点Q的坐标为(1,-4).