题目内容
已知函数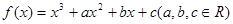 的图像过原点,且在
的图像过原点,且在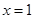 处的切线为直线
处的切线为直线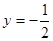
(Ⅰ)求函数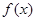 的解析式;
的解析式;
(Ⅱ)求函数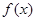 在区间
在区间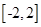 上的最小值和最大值.
上的最小值和最大值.
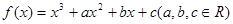 的图像过原点,且在
的图像过原点,且在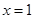 处的切线为直线
处的切线为直线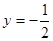
(Ⅰ)求函数
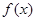 的解析式;
的解析式;(Ⅱ)求函数
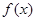 在区间
在区间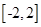 上的最小值和最大值.
上的最小值和最大值.(Ⅰ)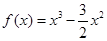 ;(Ⅱ)最小值为
;(Ⅱ)最小值为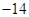 ,最大值为
,最大值为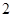 .
.
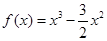 ;(Ⅱ)最小值为
;(Ⅱ)最小值为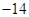 ,最大值为
,最大值为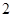 .
.试题分析:(Ⅰ)求函数
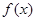 的解析式,关键是求
的解析式,关键是求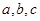 的值,因为函数
的值,因为函数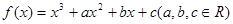 的图像过原点,故
的图像过原点,故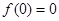 ,可得
,可得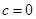 ,又因为在
,又因为在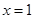 处的切线为直线
处的切线为直线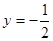 ,即在
,即在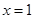 处的切线的直线斜率为
处的切线的直线斜率为 ,即
,即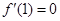 ,可得
,可得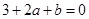 ,还需要找一个条件,切线方程为
,还需要找一个条件,切线方程为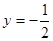 ,即
,即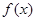 过
过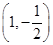 ,代入可求出
,代入可求出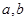 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数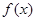 在区间
在区间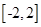 上的最小值和最大值,只需对
上的最小值和最大值,只需对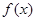 求导数,分别求出导数等零点对与端点处的函数值,比较谁最大为最大值,谁最小为最小值即可.
求导数,分别求出导数等零点对与端点处的函数值,比较谁最大为最大值,谁最小为最小值即可.试题解析:(Ⅰ)由题意
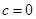 ,
,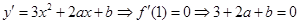
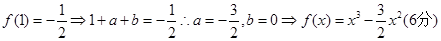
(Ⅱ)
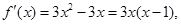 在
在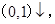 在
在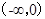 和
和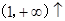

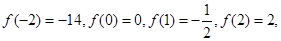 故最小值为
故最小值为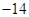 ,最大值为
,最大值为 .(12分)
.(12分)
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
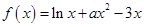 ,且在
,且在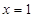 时函数取得极值.
时函数取得极值.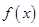 的单调增区间;
的单调增区间;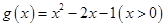 ,
,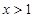 时,
时,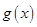 的图象恒在
的图象恒在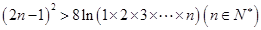 恒成立.
恒成立.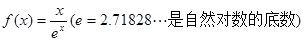 .
.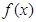 的单调区间及最大值;
的单调区间及最大值;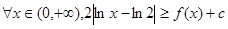 恒成立,试求实数
恒成立,试求实数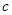 的取值范围.
的取值范围.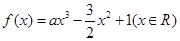 ,其中
,其中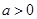 .
.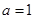 ,求曲线
,求曲线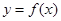 在点
在点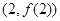 处的切线方程;
处的切线方程;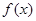 有三个零点,求
有三个零点,求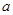 的取值范围.
的取值范围.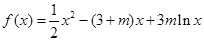 ,
,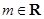 .
.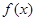 的单调递增区间;
的单调递增区间;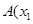 ,
,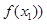 ,
,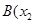 ,
,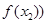 为函数
为函数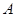 ,
,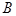 两点的直线
两点的直线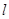 的斜率恒大于
的斜率恒大于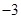 ,求
,求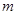 的取值范围.
的取值范围.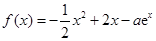 .
.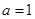 ,求
,求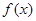 在
在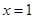 处的切线方程;
处的切线方程;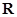 上是增函数,求实数
上是增函数,求实数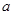 的取值范围.
的取值范围.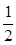 x2+(1-a)x上的一点,若曲线在M处的切线的倾斜角是均不小于
x2+(1-a)x上的一点,若曲线在M处的切线的倾斜角是均不小于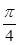 的锐角,则实数a的取值范围是________.
的锐角,则实数a的取值范围是________.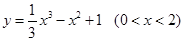 的图象上任意点处切线的倾斜角为
的图象上任意点处切线的倾斜角为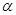 ,则
,则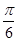
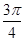
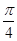
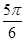
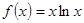 ,若
,若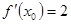 ,则x0等于 ( )
,则x0等于 ( )


