题目内容
17.现定义一种运算“⊕”:对任意实数a,b,a⊕b=$\left\{\begin{array}{l}{b,a-b≥1}\\{a,a-b<1}\end{array}\right.$,设f(x)=(x2-2x)⊕(x+3),若函数g(x)=f(x)+k的图象与x轴恰有两个公共点,则实数k的取值范围是(-3,-2)∪(-8,-7]∪{1}.分析 由条件根据新定义求得f(x)的解析式,由题意可得f(x)的图象和直线y=-k有2个交点,数形结合求得k的范围.
解答 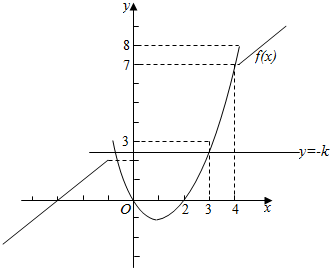 解:令(x2-2x)-(x+3)=1,
解:令(x2-2x)-(x+3)=1,
求得x=-1,或x=4,
故当x≤-1或x≥4时,
(x2-2x)-(x+3)≥1,f(x)=x+3;
当x∈(-1,4)时,
(x2-2x)-(x+3)<1,f(x)=x2-2x.
函数g(x)=f(x)+k的图象与x轴恰有两个公共点,
则f(x)的图象和直线y=-k有2个交点,
如图所示:
故有-k=-1,或2<-k<3,或 7≤-k<8,
求得实数k的取值范围为:(-3,-2)∪(-8,-7]∪{1}.
点评 本题主要考查新定义,函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.在△ABC中,a=3,$b=\sqrt{5}$,A=60°,则cosB=( )
| A. | $±\frac{{\sqrt{15}}}{6}$ | B. | $\frac{{\sqrt{15}}}{6}$ | C. | $±\frac{{\sqrt{21}}}{6}$ | D. | $\frac{{\sqrt{21}}}{6}$ |
2.复数$\frac{2-i}{i}$(i为虚数单位)在复平面内对应点的坐标是( )
| A. | (2,-1) | B. | (-2,-1) | C. | (-1,-2) | D. | (-1,2) |
6.如果a<b<0,那么下列各式一定成立的是( )
| A. | a-b>0 | B. | ac<bc | C. | a2>b2 | D. | $\frac{1}{a}$<$\frac{1}{b}$ |