题目内容
已知函数f(x)=ln
(a≠1)是奇函数.
(1)求实数a的值;
(2)求证:函数g(x)=f(x)-2x在区间[
,
]上有唯一零点(参考数据:ln3≈1.099,ln17≈2.833)
| 1-ax |
| x-1 |
(1)求实数a的值;
(2)求证:函数g(x)=f(x)-2x在区间[
| 9 |
| 8 |
| 5 |
| 4 |
考点:函数的零点,函数奇偶性的性质
专题:函数的性质及应用
分析:(1)利用奇函数的定义、对数的运算法则即可得出.
(2)先判定函数g(x)的单调性,再利用函数零点存在定理即可得出.
(2)先判定函数g(x)的单调性,再利用函数零点存在定理即可得出.
解答:
(1)解:∵函数f(x)=ln
(a≠1)为奇函数,
∴f(-x)+f(x)=ln
+ln
=ln
=0,
∴
=1,∴a2=1且a≠1,解得a=-1.
∴f(x)=ln
.
经过验证满足题意.
(2)证明:函数g(x)=f(x)-2x=ln
-2x=ln(1+
)-2x在区间[
,
]上单调递减,
且g(
)=ln17-
>0,g(
)=2ln3-
<0,
∴g(
)•g(
)<0,
因此函数g(x)在区间(
,
)由零点且有唯一零点.
| 1-ax |
| x-1 |
∴f(-x)+f(x)=ln
| 1+ax |
| -x-1 |
| 1-ax |
| x-1 |
| 1-a2x2 |
| 1-x2 |
∴
| 1-a2x2 |
| 1-x2 |
∴f(x)=ln
| x+1 |
| x-1 |
经过验证满足题意.
(2)证明:函数g(x)=f(x)-2x=ln
| x+1 |
| x-1 |
| 2 |
| x-1 |
| 9 |
| 8 |
| 5 |
| 4 |
且g(
| 9 |
| 8 |
| 9 |
| 4 |
| 5 |
| 4 |
| 5 |
| 2 |
∴g(
| 9 |
| 8 |
| 5 |
| 4 |
因此函数g(x)在区间(
| 9 |
| 8 |
| 5 |
| 4 |
点评:本题考查了奇函数的定义、对数的运算法则、函数的单调性、函数零点存在定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
已知集合A={x|1<x<5},B={x|x2-3x+2<0},则CAB=( )
| A、{x|2<x<5} |
| B、{x|2≤x<5} |
| C、{x|2≤x≤5} |
| D、∅ |
如图中O′A′B′C′为四边形OABC的斜二测直观图,则原平面图形OABC是( )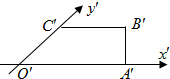
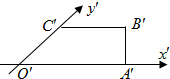
| A、直角梯形 |
| B、等腰梯形 |
| C、非直角且非等腰的梯形 |
| D、不可能是梯形 |
 设函数y=2sinx(0≤x≤п)的图象为曲线C,动点A(x,y)在曲线C上,过A且平行于x轴的直线交曲线C于点B(A、B可以重合),设线段AB的长为f(x),则函数f(x)单调递增区间
设函数y=2sinx(0≤x≤п)的图象为曲线C,动点A(x,y)在曲线C上,过A且平行于x轴的直线交曲线C于点B(A、B可以重合),设线段AB的长为f(x),则函数f(x)单调递增区间