题目内容
(本小题共16分)
已知数列 各项均不为0,其前
各项均不为0,其前 项和为
项和为 ,且对任意
,且对任意 都有
都有 (
( 为大于1的常数),记f(n)
为大于1的常数),记f(n) .
.
(1)求 ;
;
(2)试比较 与
与 的大小(
的大小( );
);
(3)求证:(2n-1)f(n)≤f(1)+f(2)+…+f(2n-1) ≤[1-()2n-1] (n∈N*)
已知数列
 各项均不为0,其前
各项均不为0,其前 项和为
项和为 ,且对任意
,且对任意 都有
都有 (
( 为大于1的常数),记f(n)
为大于1的常数),记f(n) .
.(1)求
 ;
;(2)试比较
 与
与 的大小(
的大小( );
);(3)求证:(2n-1)f(n)≤f(1)+f(2)+…+f(2n-1) ≤[1-()2n-1] (n∈N*)
(1)

(2)


 ,(
,( ).
).(3)略
解:(1) ∵ , ①
, ①
∴ . ②
. ②
②-①,得 ,即
,即 .
.
在①中令 ,可得
,可得 .
.
∴ 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列, . ……… 4分
. ……… 4分
(2).
f(n) ,
,

 .
.
而
 ,且
,且 ,
,
∴ ,
, .
.
∴

 ,(
,( ). …10分
). …10分
(3) 由(2)知 ,
,


 ,(
,( ).
).
∴当n 时,
时, .
.

 ,
,
(当且仅当 时取等号).
时取等号).
另一方面,当n ,
, 时,
时,



 .
.
∵ ,∴
,∴ .
.
∴ ,(当且仅当
,(当且仅当 时取等号).
时取等号).
∴ .
.
(当且仅当 时取等号).
时取等号).
综上所述,2n-1)f(n)≤f(1)+f(2)+…+f(2n-1) ≤[1-()2n-1] (n∈N*)
 , ①
, ①∴
 . ②
. ②②-①,得
 ,即
,即 .
.在①中令
 ,可得
,可得 .
.∴
 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列, . ……… 4分
. ……… 4分 (2).
f(n)
 ,
, 
 .
.而

 ,且
,且 ,
,∴
 ,
, .
.∴


 ,(
,( ). …10分
). …10分(3) 由(2)知
 ,
,

 ,(
,( ).
).∴当n
 时,
时, .
.
 ,
, (当且仅当
 时取等号).
时取等号).另一方面,当n
 ,
, 时,
时,


 .
.∵
 ,∴
,∴ .
.∴
 ,(当且仅当
,(当且仅当 时取等号).
时取等号).∴
 .
. (当且仅当
 时取等号).
时取等号).综上所述,2n-1)f(n)≤f(1)+f(2)+…+f(2n-1) ≤[1-()2n-1] (n∈N*)

练习册系列答案
相关题目
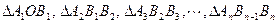 均为等腰直角三角形, 已知它们的直角顶点
均为等腰直角三角形, 已知它们的直角顶点 …,
…, 在曲线
在曲线 上,
上, 在
在 轴上(如图),
轴上(如图),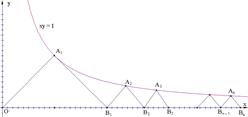
 的长;
的长; 的通项公式.
的通项公式.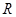 上的函数
上的函数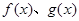 满足
满足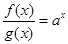 ,
,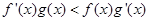 ,
, 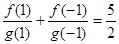 ,有穷数列
,有穷数列 (
(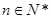 )的前
)的前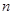 项和等于
项和等于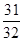 , 则n等于
, 则n等于 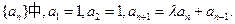
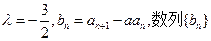 是公比为β的等比数列,求α和β的值。
是公比为β的等比数列,求α和β的值。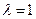 ,基于事实:如果d是a和b的公约数,那么d一定是a-b的约数。研讨是否存在正整数k和n,使得
,基于事实:如果d是a和b的公约数,那么d一定是a-b的约数。研讨是否存在正整数k和n,使得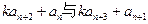 有大于1的公约数,如果存在求出k和n,如果不存在请说明理由。
有大于1的公约数,如果存在求出k和n,如果不存在请说明理由。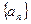 中,
中, ,
, ,令
,令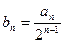 ,
,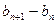 的值 (2)求
的值 (2)求 的前
的前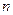 项和.(10分)
项和.(10分)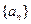 的前
的前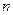 项和为
项和为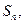
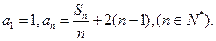
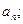

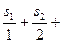
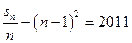 ?若存在,求出
?若存在,求出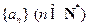 满足:
满足: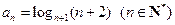 ,定义使
,定义使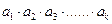 为整数的数
为整数的数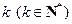 叫做企盼数,则区间
叫做企盼数,则区间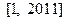 内所有的企盼数的和为
内所有的企盼数的和为  项的和
项的和 等于 .
等于 .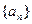 中,若
中,若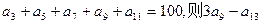 的值为( )
的值为( )