题目内容
已知定义在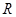 上的函数
上的函数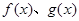 满足
满足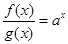 ,
,
且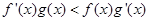 ,
, 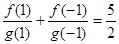 ,有穷数列
,有穷数列 (
(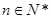 )的前
)的前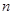 项和等于
项和等于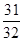 , 则n等于
, 则n等于
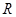 上的函数
上的函数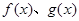 满足
满足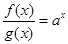 ,
,且
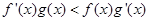 ,
, 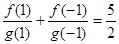 ,有穷数列
,有穷数列 (
(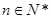 )的前
)的前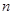 项和等于
项和等于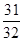 , 则n等于
, 则n等于 | A.4 | B.5 | C.6 | D.7 |
B
本题考查导数的运算会利用导数判定函数的单调性,指数函数的性质,等比数列的定义和前n项和.
因为 ,又
,又 ,所以
,所以 ,则函数
,则函数 是减函数;根据
是减函数;根据 ,即
,即 解得公比
解得公比 (舍去);于是
(舍去);于是 ,显然数列
,显然数列 是首项为
是首项为 ,公比为的
,公比为的 等比数列;前n项和为
等比数列;前n项和为 ,解得
,解得 故选B
故选B
因为
 ,又
,又 ,所以
,所以 ,则函数
,则函数 是减函数;根据
是减函数;根据 ,即
,即 解得公比
解得公比 (舍去);于是
(舍去);于是 ,显然数列
,显然数列 是首项为
是首项为 ,公比为的
,公比为的 等比数列;前n项和为
等比数列;前n项和为 ,解得
,解得 故选B
故选B
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前
的前 项和为
项和为 ,若
,若 ,且A、B、C三点共线(该直线不过原点
,且A、B、C三点共线(该直线不过原点 ),则
),则 =( )
=( ) 各项均不为0,其前
各项均不为0,其前 项和为
项和为 ,且对任意
,且对任意 都有
都有 (
( 为大于1的常数),记f(n)
为大于1的常数),记f(n) .
. ;
; 与
与 的大小(
的大小(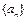 的前
的前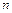 项和为
项和为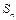 ,
,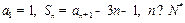 .
.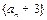 是等比数列;
是等比数列;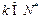 ,设
,设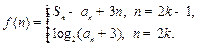 求使不等式
求使不等式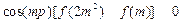 成立的正整数
成立的正整数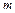 的取值范围.
的取值范围.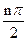 )an+sin
)an+sin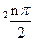 ,n=1.2.3…
,n=1.2.3…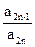 ,令 Sn=
,令 Sn=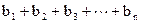 ,求 Sn
,求 Sn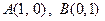 和互不相同的点
和互不相同的点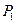 ,
, ,
,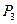 ,…,
,…, ,…,满足
,…,满足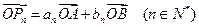 ,
,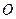 为坐标原点,其中
为坐标原点,其中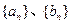 分别为等差数列和等比数列,若
分别为等差数列和等比数列,若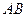 的中点,设等差数列公差为
的中点,设等差数列公差为 ,等比数列公比为
,等比数列公比为 ,当
,当 中,
中, ,则数列
,则数列