题目内容
已知矩形的周长为36，矩形绕它的一条边旋转形成一个圆柱，则旋转形成的圆柱的侧面积的最大值为 ．
考点：基本不等式
专题：不等式的解法及应用
分析：利用矩形的周长公式、基本不等式的性质、圆柱的侧面积计算公式即可得出．
解答：
解：如图所示，
设矩形的长与宽分别为a，b．
则2a+2b=36，即a+b=18．
∴18≥2
，当且仅当a=b=9时取等号．
解得ab≤81．
∴旋转形成的圆柱的侧面积=π•2a•b≤2π•81=162π．
∴旋转形成的圆柱的侧面积的最大值为162π．
故答案为：162π．
设矩形的长与宽分别为a，b．
则2a+2b=36，即a+b=18．
∴18≥2
| ab |
解得ab≤81．
∴旋转形成的圆柱的侧面积=π•2a•b≤2π•81=162π．
∴旋转形成的圆柱的侧面积的最大值为162π．
故答案为：162π．
点评：本题考查了矩形的周长公式、基本不等式的性质、圆柱的侧面积计算公式，属于基础题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知f（x）=3x2+2x+1，若
f（x）dx=2f（a），那么a=（ ）
| ∫ | 1 -1 |
| A、-1 | ||
B、
| ||
C、-1或
| ||
| D、1 |
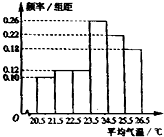如图是根据部分城市某年6月份的平均气温（单位：℃）数据得到的样本频率分布直方图，其中平均气温的范围是[20.5，26.5]，样本数据的分组为[20.5，21.5），[21.5，22.5），[22.5，23.5），[23.5，24.5），[24.5，25.5），[25.5，26.5]．已知样本中平均气温低于22.5℃的城市个数为11，则样本中平均气温不低于25.5℃的城市个数为（ ）y=f（x）满足2f（x）+f（
）=lnx，则函数f（x）在x=1处的切线斜率为（ ）
| 1 |
| x |
| A、1 | B、2 | C、3 | D、4 |
若不等式（m-1）x2+（m-1）x+2＞0的解集是R，则m的范围是（ ）
| A、（1，9） |
| B、（-∞，1]∪（9，+∞） |
| C、[1，9） |
| D、（-∞，1）∪（9，+∞） |