题目内容
P为圆A: 上的动点,点B(1,0).线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为
上的动点,点B(1,0).线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为 .
.
(I)求曲线 的方程;
的方程;
(II)当点P在第一象限,且cos∠BAP= 时,求点M的坐标.
时,求点M的坐标.
解:
(Ⅰ)圆A的圆心为A(-1,0),半径等于2 .
.
由已知|MB|=|MP|,于是|MA|+|MB|=|MA|+|MP|=2 ,
,
故曲线Γ是以A,B为焦点,以2 为长轴长的椭圆,a=
为长轴长的椭圆,a= ,c=1,b=1,
,c=1,b=1,
曲线Γ的方程为 +y2=1.
+y2=1.
(Ⅱ)由cos∠BAP= ,|AP|=2
,|AP|=2 ,得P(
,得P( ,
, ).
).
于是直线AP方程为y= (x+1).
(x+1).
由 解得5x2+2x-7=0,x1=1,x2=-
解得5x2+2x-7=0,x1=1,x2=- .
.
由于点M在线段AP上,所以点M坐标为(1, ).
).

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
 .
. ,动点
,动点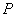 满足
满足 ,则
,则 的最大
的最大
 =(1, x ),
=(1, x ), =(x-1, 2), 若
=(x-1, 2), 若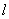 交抛物线C于A、B两点,若A到抛物线的准线的距离为4,则|AB|= .
交抛物线C于A、B两点,若A到抛物线的准线的距离为4,则|AB|= . ,复数
,复数 的实部为
的实部为 ,虚部为1,则
,虚部为1,则 的取值范围是( )
的取值范围是( ) D.
D.
 C.
C.  D.
D. 

 等于
等于 B.
B. C.
C.  D.
D.
 值为
值为 
 D.
D.