题目内容
球O是四面体ABCD的外接球(即四面体的顶点均在球面上),若DB⊥平面ABC,AB⊥AC,且AC=1,DB=AB=2,则球O的表面积为( )
| A、10π | B、9π | C、8π | D、7π |
考点:直线与平面垂直的性质,球内接多面体
专题:空间位置关系与距离
分析:构造长方体,则长方体的外接球和四面体的外接球是相同的,由长方体的体对角线等于球的直径2R可求得2R=
=
=3,从而求得R的值,即可求得球O的表面积.
| 12+22+22 |
| 9 |
解答:
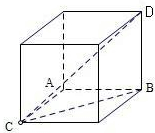 解:∵DB⊥平面ABC,AB⊥AC,且AC=1,DB=AB=2,
解:∵DB⊥平面ABC,AB⊥AC,且AC=1,DB=AB=2,
∴构造长方体,则长方体的外接球和四面体的外接球是相同的,
则长方体的体对角线等于球的直径2R,
则2R=
=
=3,
∴R=
,
则球O的表面积为4πR2=4π×(
)2=9π,
故选:B.
 解:∵DB⊥平面ABC,AB⊥AC,且AC=1,DB=AB=2,
解:∵DB⊥平面ABC,AB⊥AC,且AC=1,DB=AB=2,∴构造长方体,则长方体的外接球和四面体的外接球是相同的,
则长方体的体对角线等于球的直径2R,
则2R=
| 12+22+22 |
| 9 |
∴R=
| 3 |
| 2 |
则球O的表面积为4πR2=4π×(
| 3 |
| 2 |
故选:B.
点评:本题主要考查了直线与平面垂直的性质,球内接多面体,根据已知构造一个长方体是解题的关键,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知函数f(x)=
,则f(x)的最小值为( )
|
| A、-4 | ||
| B、2 | ||
C、2
| ||
| D、4 |
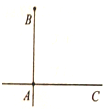 如图,两高速公路线垂直相交于站A,若已知AB=100千米,甲汽车从A站出发,沿AC方向以50千米/小时的速度行驶,同时乙汽车从B站出发,一年BA方向以v千米/小时的速度行驶,至A站即停止前行(甲车仍继续行驶)(两车的车长忽略不计).
如图,两高速公路线垂直相交于站A,若已知AB=100千米,甲汽车从A站出发,沿AC方向以50千米/小时的速度行驶,同时乙汽车从B站出发,一年BA方向以v千米/小时的速度行驶,至A站即停止前行(甲车仍继续行驶)(两车的车长忽略不计). 某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.