题目内容
3.要得到函数 f(x)=sin(3x+$\frac{π}{3}$)的导函数f′(x)的图象,只需将f(x)的图象( )| A. | 向右平移$\frac{π}{3}$个单位,再把各点的纵坐标伸长到原来的3倍( 横坐标不变) | |
| B. | 向右平移$\frac{π}{6}$个单位,再把各点的纵坐标缩短到原来的3倍( 横坐标不变) | |
| C. | 向左平移$\frac{π}{3}$个单位,再把各点的纵坐标缩短到原来的 3倍( 横坐标不变) | |
| D. | 向左平移$\frac{π}{6}$个单位,再把各点的纵坐标伸长到原来的 3倍( 横坐标不变) |
分析 求导,根据同角的正弦函数图象向左平移四分之一个周期可得同角的余弦函数图象,结合纵向伸缩变换的法则,可得答案.
解答 解:∵函数 f(x)=sin(3x+$\frac{π}{3}$),
∴f′(x)=3cos(3x+$\frac{π}{3}$),
要得到函数f′(x)的图象,只需将f(x)的图象:
向左平移$\frac{π}{6}$个单位得到y=cos(3x+$\frac{π}{3}$)的图象,
再保持 横坐标不变把各点的纵坐标伸长到原来的 3倍,
故选:D
点评 本题考查的知识点是导数的运算,函数图象的平移变换和伸缩变换,难度中档.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
13.下列命题中,是假命题的是( )
| A. | ?x>0,x>lnx | B. | ?x0∈R,tanx0=2016 | ||
| C. | ?x0∈R,sinx0+cosx0=$\sqrt{3}$ | D. | ?x∈R,2x>0 |
11.双曲线 $\frac{x^2}{4}-\frac{y^2}{16}=1$的一条渐近线方程为( )
| A. | y=2x | B. | $y=\frac{1}{2}x$ | C. | y=4x | D. | $y=\frac{1}{4}x$ |
18.设k∈R,动直线l1:kx-y+k=0过定点A,动直线l2:x+ky-5-8k=0过定点B,并且l1与l2相交于点P,则|PA|+|PB|的最大值为( )
| A. | $10\sqrt{2}$ | B. | $5\sqrt{2}$ | C. | $10\sqrt{5}$ | D. | $5\sqrt{5}$ |
8.若实数x,y满足约束条件$\left\{\begin{array}{l}{x+y≥1}\\{x-y≥-1}\\{2x-y≤2}\end{array}\right.$,则目标函数z=2x+y的最小值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
2.已知在△ABC中,a,b,c分别是∠BAC,∠ABC,∠ACB的对边,若过点C作垂直于AB的垂线CD,且CD=h,则下列给出的关于a,b,c,h的不等式中正确的是( )
| A. | a+b≥$\sqrt{2{h}^{2}+2{c}^{2}}$ | B. | a+b≥$\sqrt{4{h}^{2}+{c}^{2}}$ | C. | a+b≥$\sqrt{4{h}^{2}+2{c}^{2}}$ | D. | a+b≥$\sqrt{{h}^{2}+2{c}^{2}}$ |
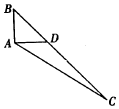 如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}$=3$\overrightarrow{BD}$,|$\overrightarrow{AD}$|=1,则$\overrightarrow{AC}$•$\overrightarrow{AD}$的值为( )
如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}$=3$\overrightarrow{BD}$,|$\overrightarrow{AD}$|=1,则$\overrightarrow{AC}$•$\overrightarrow{AD}$的值为( )