题目内容
1.在下列函数中既是奇函数,又是在区间(0,+∞)上单调递减的函数为( )| A. | $y=ln\frac{1}{|x|}$ | B. | y=x-1 | C. | $y={({\frac{1}{2}})^x}$ | D. | y=x3+x |
分析 根据奇函数、偶函数的定义,和奇函数图象的对称性,以及函数y=x3和y=x的单调性即可判断每个选项的正误,从而找出正确选项.
解答 解:A.函数$y=ln\frac{1}{|x|}$为偶函数,不是奇函数,∴该选项错误;
B.反比例函数y=x-1是奇函数,且在(0,+∞)上单调递减,∴该选项正确;
C.指数函数$y=(\frac{1}{2})^{x}$的图象不关于原点对称,不是奇函数,∴该选项错误;
D.y=x3和y=x在区间(0,+∞)上都单调递增,∴y=x3+x在(0,+∞)上单调递增,∴该选项错误.
故选B.
点评 考查奇函数、偶函数的定义,奇函数图象的对称性,反比例函数的单调性,以及y=x3和y=x的单调性.

练习册系列答案
相关题目
8.不等式组$\left\{\begin{array}{l}{x-y≤0}\\{x+y≥-2}\\{x-2y≥-2}\end{array}\right.$的解集记为D,若(a,b)∈D,则z=2a-3b的最大值是( )
| A. | 1 | B. | 4 | C. | -1 | D. | -4 |
9.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是( )
| A. | y=x3 | B. | y=|x+1| | C. | y=-x2 | D. | y=|x|+1 |
6.用边长为120cm的正方形铁皮做一个无盖水箱,先在四周分别截去一个小正方形,然后把四边翻转90°角,再焊接成水箱,则水箱的最大容积为( )
| A. | 120 000 cm3 | B. | 128 000 cm3 | C. | 150 000 cm3 | D. | 158 000 cm3 |
11.命题p:?φ∈R,函数f(x)=sin(2x+φ)不是偶函数,则¬p为( )
| A. | ?φ∈R,函数f(x)=sin(2x+φ)是奇函数 | B. | ?φ∈R,函数f(x)=sin(2x+φ)不是偶函数 | ||
| C. | ?φ∈R,函数f(x)=sin(2x+φ)是偶函数 | D. | ?φ∈R,函数f(x)=sin(2x+φ)是偶函数 |
 函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)解析式f(x)=2sin(2x-$\frac{π}{3}$).
函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)解析式f(x)=2sin(2x-$\frac{π}{3}$).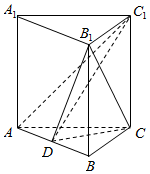 如图,在三棱柱ABC-A1B1C1中,AC=4,BC=3,AB=B1C=5,点D是线段AB的中点,四边形ACC1A1为正方形.
如图,在三棱柱ABC-A1B1C1中,AC=4,BC=3,AB=B1C=5,点D是线段AB的中点,四边形ACC1A1为正方形.

 如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).
如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).