题目内容
15．从圆x2+y2=4内任取一点p，则p到直线x+y=1的距离小于$\frac{\sqrt{2}}{2}$的概率$\frac{π+2}{4π}$．分析 利用点到直线的距离公式求出满足条件的点的弧长、几何概型的计算公式即可得出．
解答 解：由点到直线的距离公式得点O到直线x+y=1的距离为$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$，
故到直线x+y=1距离为$\frac{\sqrt{2}}{2}$的点在直线x+y=0和x+y+2=0上，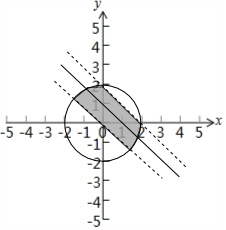
满足P到直线x+y=1的距离小于$\frac{\sqrt{2}}{2}$的点位于两直线之间的弧上，且两段弧度和为90°．
故概率P=$\frac{\frac{1}{4}×4π+\frac{1}{2}×2×2}{4π}$=$\frac{π+2}{4π}$．
故答案为：$\frac{π+2}{4π}$
点评 熟练掌握点到直线的距离公式及几何概型的计算公式是解题的关键．
练习册系列答案
相关题目
5．
某制造商为运动会生产一批直径为40mm的乒乓球，现随机抽样检查20只，测得每只球的直径（单位：mm，保留两位小数）如下：
（Ⅰ）完成下面的频率分布表，并画出频率分布直方图；
（Ⅱ）假定乒乓球的直径误差不超过0.02mm为合格品，若这批乒乓球的总数为10 000只，试根据抽样检查结果估计这批产品的合格只数．
某制造商为运动会生产一批直径为40mm的乒乓球，现随机抽样检查20只，测得每只球的直径（单位：mm，保留两位小数）如下：| 40.02 | 40.00 | 39.98 | 40.00 | 39.99 |
| 40.00 | 39.98 | 40.01 | 39.98 | 39.99 |
| 40.00 | 39.99 | 39.95 | 40.01 | 40.02 |
| 39.98 | 40.00 | 39.99 | 40.00 | 39.96 |
| 分组 | 频数 | 频率 | $\frac{频率}{组距}$ |
| [39.95，39.97） | 2 | ||
| [39.97，39.99） | 4 | ||
| [39.99，40.01） | 10 | ||
| [40.01，40.03] | 4 | ||
| 合计 |
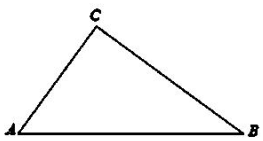如图，A，B，C三地有直道相通，AB=10 千米，AC=6 千米，BC=8千米．现甲、乙两人同时从A地出发匀速前往B地，经过t小时，他们之间的距离为f（t）（单位：千米）．甲的路线是AB，速度为10千米/小时，乙的路线是ACB，速度为16千米/小时．乙到达B地后原地等待．设t=t1时乙到达C地．
10．若集合A={x|x2+3x-4＞0}，集合B={x|-1＜x≤3}，且M=A∩B，则有（ ）
| A． | -1∈M | B． | 0∈M | C． | 1∈M | D． | 2∈M |
已知函数f（x）=x2+2x|x-a|，其中a∈R．