题目内容
1．若抛物线y2=2px的焦点坐标为（4，0），则其准线方程为（ ）| A． | x=-2 | B． | x=-4 | C． | x=-8 | D． | x=-16 |
分析 利用抛物线的准线方程求解即可．
解答 解：由于抛物线y2=2px的焦点坐标为（4，0），
则$\frac{p}{2}$=4，
解得p=8，
则其准线方程为x=-4，
故选：B
点评 本题考查抛物线的简单性质的应用，基本知识的考查．
练习册系列答案
相关题目
11．若集合A={x|x2≤0}，则下列结论中正确的是（ ）
| A． | A=0 | B． | 0⊆A | C． | A=∅ | D． | {0}⊆A |
12．以点（2，-1）为圆心，且被直线x+y-6=0截得弦长为$\sqrt{30}$的圆的方程是（ ）
| A． | （x+2）2+（y-1）2=40 | B． | （x-2）2+（y+1）2=40 | C． | （x+2）2+（y-1）2=20 | D． | （x-2）2+（y+1）2=20 |
9．已知函数f（x）=kx2-3x+1的图象与x轴在原点的右侧有公共点，则实数k的取值范围为（ ）
| A． | （0，$\frac{9}{4}$） | B． | [0，$\frac{9}{4}$] | C． | （-∞，$\frac{9}{4}$） | D． | （-∞，$\frac{9}{4}$] |
16．已知i是虚数单位，则复数i（1+i）等于（ ）
| A． | 1+i | B． | 1-i | C． | -1+i | D． | -1-i |
6．
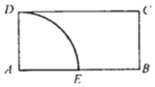如图，在矩形ABCD中，AD=1，AB=2，以A为圆心，AD为半径在矩形内部作扇形AED，若向矩形ABCD内部随机投放一点，则所投点落在扇形外部的概率为（ ）
如图，在矩形ABCD中，AD=1，AB=2，以A为圆心，AD为半径在矩形内部作扇形AED，若向矩形ABCD内部随机投放一点，则所投点落在扇形外部的概率为（ ）| A． | $\frac{π}{8}$ | B． | 1-$\frac{π}{8}$ | C． | $\frac{π}{4}$ | D． | 1-$\frac{π}{4}$ |
10．函数f（x）=2mx+4，若在[-2，1]内恰有一个零点，则m的取值范围是（ ）
| A． | [-1，2] | B． | [1，+∞） | C． | （-∞，-2]∪[1，+∞） | D． | [-2，1] |
11．利用计算机产生0～1之间的均匀随机数a，则事件“3a-1＜0”发生的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{5}{6}$ |