题目内容
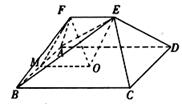
如图,在五面体,ABCDF中,点O是矩形ABCD的对角线的交点,面ABF是等边三角形,棱EF=![]() .
.
(1)证明EO∥平面ABF;
(2)问![]() 为何值时,有OF⊥ABE,试证明你的结论.
为何值时,有OF⊥ABE,试证明你的结论.
(Ⅰ)证明见解析(Ⅱ)![]()
解析:
(1)证明:取AB中点M,连结OM. 2分
 在矩形ABCD中,OM=
在矩形ABCD中,OM=![]() ,
,
又EF=![]() ,则EF=OM,
,则EF=OM,
连结FM,于是四边形EFMO为平行四边形.∴OE∥FM. 4分
又∵EO![]() 平面ABF,FM
平面ABF,FM![]() 平面ABF,∴EO∥平面ABF. 6分
平面ABF,∴EO∥平面ABF. 6分
(2)解:∵OF⊥平面ABE,连结EM.
∵EM![]() 平面ABE.∴OF⊥EM,又四边形OEFM为平行四边形.
平面ABE.∴OF⊥EM,又四边形OEFM为平行四边形.
∴□OEFM为菱形. 8分
∴OM=MF,设OM=a,则BC=2a.
在正△ABF中,MF=a,∴a=![]() ,∴
,∴![]() . 10分
. 10分
∴CD=![]() ,∴
,∴
综上可知,当![]() 时,有OF⊥平面ABE. 12分
时,有OF⊥平面ABE. 12分

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
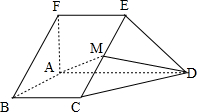 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=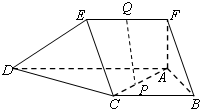 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,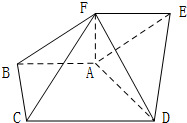 如图,在五面体ABCDEF中,AB∥DC,
如图,在五面体ABCDEF中,AB∥DC,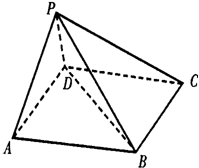 如图,在五面体P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,PB=
如图,在五面体P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,PB= 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=