题目内容
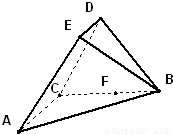
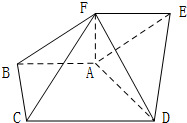 如图,在五面体ABCDEF中,AB∥DC,∠BAD=
如图,在五面体ABCDEF中,AB∥DC,∠BAD=| π |
| 2 |
| 7 |
(Ⅰ)直线AB到平面EFCD的距离;
(Ⅱ)二面角F-AD-E的平面角的正切值.
分析:解法一:(几何法)(Ⅰ)AB到面EFCD的距离等于点A到面EFCD的距离,故可过A作平面EFCD的垂线,注意到面AFD⊥面EFDC,故只需过A作FD的垂线即可.
(Ⅱ)由已知条件做出二面角F-AD-E的平面角,再求解.已知FA⊥AD,再可求证EA⊥AD,故,∠FAE为二面角F-AD-E的平面角,再解△AEF即可.
解法二:(向量法)由AB、AD、AF两两垂直,故可通过向量法求解.
(Ⅰ)求平面EFCD的法向量
,则直线AB到平面EFCD的距离=
(Ⅱ)分别求出两个面的法向量,再求两个法向量的余弦,即二面角F-AD-E的平面角的余弦,再求正切即可.
(Ⅱ)由已知条件做出二面角F-AD-E的平面角,再求解.已知FA⊥AD,再可求证EA⊥AD,故,∠FAE为二面角F-AD-E的平面角,再解△AEF即可.
解法二:(向量法)由AB、AD、AF两两垂直,故可通过向量法求解.
(Ⅰ)求平面EFCD的法向量
| m |
| ||||
|
|
(Ⅱ)分别求出两个面的法向量,再求两个法向量的余弦,即二面角F-AD-E的平面角的余弦,再求正切即可.
解答: 解:法一:
解:法一:
(Ⅰ)∵AB∥DC,DC?平面EFCD,
∴AB到面EFCD的距离等于点A到面EFCD的距离,
过点A作AG⊥FD于G,因∠BAD=
AB∥DC,
故CD⊥AD;又∵FA⊥平面ABCD,
由三垂线定理可知,CD⊥FD,
故CD⊥面FAD,知CD⊥AG,
所以AG为所求直线AB到面EFCD的距离.
在Rt△FCD中,FD=
=
=
由FA⊥平面ABCD,得FA⊥AD,从而在Rt△FAD中
FA=
=
=1
∴AG=
=
=
.
即直线AB到平面EFCD的距离为
.
(Ⅱ)由己知,FA⊥平面ABCD,得FA⊥AD,
又由∠BAD=
,知AD⊥AB,
故AD⊥平面ABFE∴DA⊥AE,
所以,∠FAE为二面角F-AD-E的平面角,记为θ.
在Rt△AED中,AE=
=
=
,
由平行四边形ABCD得,FE∥BA,从而∠AFE=
在Rt△AEF中,FE=
=
=
,
故tanθ=
=
所以二面角F-AD-E的平面角的正切值为
.
法二:
(Ⅰ)如图以A点为坐标原点,
,
,
的方向为x,y,z的正方向建立空间直角坐标系数,则A(0,0,0)
C(2,2,0)D(0,2,0)设F(0,0,z0)(z0>0)可得
=(2,2,-z0),
由|
|=3.即
=3,
解得F(0,0,1)
∵AB∥DC,DC?面EFCD,
所以直线AB到面EFCD的距离等于点A到面EFCD的距离.
设A点在平面EFCD上的射影点为G(x1,y1,z1),
则
=(
,y1,z1)因
•
=0且
•
=0,
而
=(0,-2,1)
=(-2,0,0),
此即
解得x1=0①,知G点在yoz面上,
故G点在FD上.
∥
,
=(-
,-y1,-z1+1)
故有
=-z 1+1②联立①,②解得,G(0,
,
)
∴|
|为直线AB到面EFCD的距离.
而
=(0,
,
)所以|
|=
(Ⅱ)因四边形ABFE为平行四边形,
则可设E(x0,0,1)(x0<0),
=(-x0,2,-1).
由|
|=
得
=
,
解得x 0=-
.即E(-
,0,1).故
=(-
,0,1)
由
=(0,2,0),
=(0,0,1)
因
•
=0,
•
=0,
故∠FAE为二面角F-AD-E的平面角,
又∵
=(
,0,0),|
|=
,|
|=1,
所以tan∠FAE=
=
 解:法一:
解:法一:(Ⅰ)∵AB∥DC,DC?平面EFCD,
∴AB到面EFCD的距离等于点A到面EFCD的距离,
过点A作AG⊥FD于G,因∠BAD=
| π |
| 2 |
故CD⊥AD;又∵FA⊥平面ABCD,
由三垂线定理可知,CD⊥FD,
故CD⊥面FAD,知CD⊥AG,
所以AG为所求直线AB到面EFCD的距离.
在Rt△FCD中,FD=
| FC2-CD2 |
| 9-4 |
| 5 |
由FA⊥平面ABCD,得FA⊥AD,从而在Rt△FAD中
FA=
| FD2-AD2 |
| 5-4 |
∴AG=
| FA•AD |
| FD |
| 2 | ||
|
2
| ||
| 5 |
即直线AB到平面EFCD的距离为
2
| ||
| 5 |
(Ⅱ)由己知,FA⊥平面ABCD,得FA⊥AD,
又由∠BAD=
| π |
| 2 |
故AD⊥平面ABFE∴DA⊥AE,
所以,∠FAE为二面角F-AD-E的平面角,记为θ.
在Rt△AED中,AE=
| ED2-AD2 |
| 7-4 |
| 3 |
由平行四边形ABCD得,FE∥BA,从而∠AFE=
| π |
| 2 |
在Rt△AEF中,FE=
| AE2-AF2 |
| 3-1 |
| 2 |
故tanθ=
| FE |
| FA |
| 2 |
所以二面角F-AD-E的平面角的正切值为
| 2 |
法二:
(Ⅰ)如图以A点为坐标原点,
| AB |
| AD |
| AF |
C(2,2,0)D(0,2,0)设F(0,0,z0)(z0>0)可得
| FC |
由|
| FC |
22+22+
|
解得F(0,0,1)
∵AB∥DC,DC?面EFCD,
所以直线AB到面EFCD的距离等于点A到面EFCD的距离.
设A点在平面EFCD上的射影点为G(x1,y1,z1),
则
| AG |
| x | 1 |
| AG |
| DF |
| AG |
| CD |
而
| DF |
| CD |
此即
|
故G点在FD上.
| GF |
| DF |
| GF |
| x | 1 |
故有
| y1 |
| 2 |
| 2 |
| 5 |
| 4 |
| 5 |
∴|
| AG |
而
| AG |
| 2 |
| 5 |
| 4 |
| 5 |
| AG |
2
| ||
| 5 |
(Ⅱ)因四边形ABFE为平行四边形,
则可设E(x0,0,1)(x0<0),
| ED |
由|
| ED |
| 7 |
|
| 7 |
解得x 0=-
| 2 |
| 2 |
| AE |
| 2 |
由
| AD |
| AF |
因
| AD |
| AE |
| AD |
| AF |
故∠FAE为二面角F-AD-E的平面角,
又∵
| EF |
| 2 |
| EF |
| 2 |
| AF |
所以tan∠FAE=
|
| ||
|
|
| 2 |
点评:本题考查空间的角和空间距离的计算,考查空间想象能力和运算能力.注意几何法和向量法的应用.

练习册系列答案
相关题目
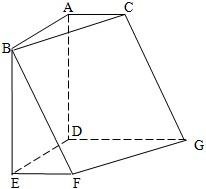 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1. 如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=
如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=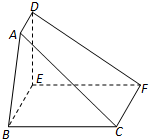 如图,在五面体ABC-DEF中,四边形BCFE 是矩形,DE⊥平面BCFE.
如图,在五面体ABC-DEF中,四边形BCFE 是矩形,DE⊥平面BCFE. ,AC=BC=2ED=2,AC⊥BC,且ED∥AC
,AC=BC=2ED=2,AC⊥BC,且ED∥AC  ,求二面角F-AE-B的余弦值.
,求二面角F-AE-B的余弦值.