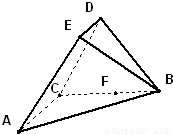
题目内容
 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=| 1 | 2 |
(1)求异面直线BF与DE所成的角的大小;
(2)求二面角A-CD-E的余弦值.
分析:(1)先将BF平移到CE,则∠CED(或其补角)为异面直线BF与DE所成的角,在三角形CED中求出此角即可;
(2)设Q为CD的中点,连接PQ,EQ,易证∠EQP为二面角A-CD-E的平面角,在直角三角形EQP中求出此角即可
(2)设Q为CD的中点,连接PQ,EQ,易证∠EQP为二面角A-CD-E的平面角,在直角三角形EQP中求出此角即可
解答: 解:(1)由题设知,BF∥CE,
解:(1)由题设知,BF∥CE,
所以∠CED(或其补角)为异面直线BF与DE所成的角.
设P为AD的中点,连接EP,PC.
因为FE=∥AP,所以FA=∥EP,同理AB=∥PC.
又FA⊥平面ABCD,所以EP⊥平面ABCD.
而PC,AD都在平面ABCD内,
故EP⊥PC,EP⊥AD.由AB⊥AD,可得PC⊥AD设FA=a,
则EP=PC=PD=a,CD=DE=EC=
a,故∠CED=60°.
所以异面直线BF与DE所成的角的大小为60°.
(2)取CD的中点Q,连接PQ,EQ
由PC=PD,CE=DE
∴PQ⊥CD,EQ⊥CD
∴∠EQP为二面角A-CD-E的平面角,
由ED=CD=
a,在等边△ECD中EQ=
a
在等腰Rt△CPD中,PQ=
a
在Rt△EPQ中,cos∠EQP=
=
.
故二面角A-CD-E的余弦值为
.
 解:(1)由题设知,BF∥CE,
解:(1)由题设知,BF∥CE,所以∠CED(或其补角)为异面直线BF与DE所成的角.
设P为AD的中点,连接EP,PC.
因为FE=∥AP,所以FA=∥EP,同理AB=∥PC.
又FA⊥平面ABCD,所以EP⊥平面ABCD.
而PC,AD都在平面ABCD内,
故EP⊥PC,EP⊥AD.由AB⊥AD,可得PC⊥AD设FA=a,
则EP=PC=PD=a,CD=DE=EC=
| 2 |
所以异面直线BF与DE所成的角的大小为60°.
(2)取CD的中点Q,连接PQ,EQ
由PC=PD,CE=DE
∴PQ⊥CD,EQ⊥CD
∴∠EQP为二面角A-CD-E的平面角,
由ED=CD=
| 2 |
| ||
| 2 |
在等腰Rt△CPD中,PQ=
| ||
| 2 |
在Rt△EPQ中,cos∠EQP=
| PO |
| EQ |
| ||
| 3 |
故二面角A-CD-E的余弦值为
| ||
| 3 |
点评:本小题考查线线垂直、二面角等基础知识,考查用空间向量解决立体几何问题的方法,考查空间想像能力、运算能力和推理论证能力.

练习册系列答案
相关题目
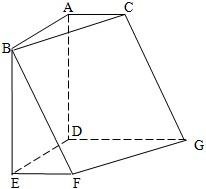 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1. 如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=
如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=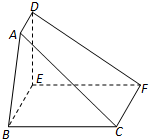 如图,在五面体ABC-DEF中,四边形BCFE 是矩形,DE⊥平面BCFE.
如图,在五面体ABC-DEF中,四边形BCFE 是矩形,DE⊥平面BCFE. ,AC=BC=2ED=2,AC⊥BC,且ED∥AC
,AC=BC=2ED=2,AC⊥BC,且ED∥AC  ,求二面角F-AE-B的余弦值.
,求二面角F-AE-B的余弦值.