题目内容
已知M (-3,0)﹑N (3,0),P为坐标平面上的动点,且直线PM与直线PN的斜率之积为常数m (m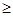
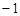 ,m
,m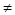 0),点P的轨迹加上M、N两点构成曲线C.
0),点P的轨迹加上M、N两点构成曲线C.
求曲线C的方程并讨论曲线C的形状;
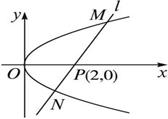
(2) 若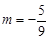 ,曲线C过点Q (2,0) 斜率为
,曲线C过点Q (2,0) 斜率为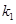 的直线
的直线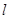 与曲线C交于不同的两点A﹑B,AB中点为R,直线OR (O为坐标原点)的斜率为
与曲线C交于不同的两点A﹑B,AB中点为R,直线OR (O为坐标原点)的斜率为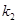 ,求证
,求证 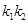 为定值;
为定值;
(3) 在(2)的条件下,设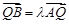 ,且
,且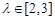 ,求
,求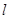 在y轴上的截距的变化范围.
在y轴上的截距的变化范围.
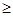
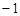 ,m
,m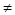 0),点P的轨迹加上M、N两点构成曲线C.
0),点P的轨迹加上M、N两点构成曲线C.求曲线C的方程并讨论曲线C的形状;
(2) 若
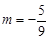 ,曲线C过点Q (2,0) 斜率为
,曲线C过点Q (2,0) 斜率为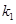 的直线
的直线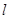 与曲线C交于不同的两点A﹑B,AB中点为R,直线OR (O为坐标原点)的斜率为
与曲线C交于不同的两点A﹑B,AB中点为R,直线OR (O为坐标原点)的斜率为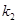 ,求证
,求证 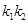 为定值;
为定值;(3) 在(2)的条件下,设
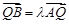 ,且
,且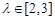 ,求
,求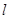 在y轴上的截距的变化范围.
在y轴上的截距的变化范围.(1)
若m=-1,则方程为 ,轨迹为圆;
,轨迹为圆;
若 ,方程为
,方程为 ,轨迹为椭圆;
,轨迹为椭圆;
若 ,方程为
,方程为 ,轨迹为双曲线
,轨迹为双曲线
(2)
(3)
若m=-1,则方程为
 ,轨迹为圆;
,轨迹为圆;若
 ,方程为
,方程为 ,轨迹为椭圆;
,轨迹为椭圆;若
 ,方程为
,方程为 ,轨迹为双曲线
,轨迹为双曲线(2)

(3)

试题分析:解:(1)由
 得点P的轨迹方程为:
得点P的轨迹方程为: .
.若m=-1,则方程为
 ,轨迹为圆;
,轨迹为圆;若
 ,方程为
,方程为 ,轨迹为椭圆;
,轨迹为椭圆;若
 ,方程为
,方程为 ,轨迹为双曲线。 4分
,轨迹为双曲线。 4分(2)
 时,曲线C方程为
时,曲线C方程为 ,
,设
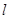 的方程为:
的方程为: ,与曲线C方程联立得:
,与曲线C方程联立得: ,
,设
 ,则
,则 ①,
①, ②,
②,可得
 , ∴
, ∴ 为定值。 7分
为定值。 7分注:①可用点差法证明;②直接用
 得出结果的,本小题只给1分.
得出结果的,本小题只给1分.(3)由
 得
得 代入①②得:
代入①②得: ③,
③, ④,
④,③式平方除以④式得:
 ,
,∵
 在
在 上单调递增,∴
上单调递增,∴ ,∴
,∴ ,可得
,可得
又∵
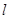 在y轴上的截距
在y轴上的截距 ,∴
,∴ =
= ,
,∴
 ,此即为
,此即为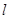 在y轴上的截距的变化范围。 10分
在y轴上的截距的变化范围。 10分点评:解决的关键是根据直线与椭圆联立方程组来结合韦达定理来求解,属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
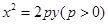 ,直线
,直线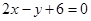 截抛物线C所得弦长为
截抛物线C所得弦长为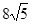 .
.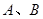 是抛物线上异于原点
是抛物线上异于原点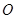 的两个动点,记
的两个动点,记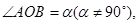 若
若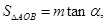 试求当
试求当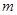 取得最小值时
取得最小值时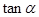 的最大值.
的最大值.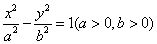 的一条渐近线方程是y=
的一条渐近线方程是y=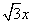 ,它的一个焦点在抛物线
,它的一个焦点在抛物线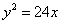 的准线上,则双曲线的方程为
的准线上,则双曲线的方程为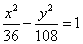
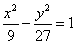

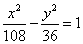
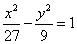
 焦点的直线与抛物线交于
焦点的直线与抛物线交于 两点,
两点, ,且
,且 中点的纵坐标为
中点的纵坐标为 ,则
,则 的值为______.
的值为______.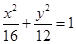 上找一点,使这一点到直线
上找一点,使这一点到直线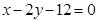 的距离为最小,并求最小值。
的距离为最小,并求最小值。 是双曲线
是双曲线 的一个焦点,则m的值为( )
的一个焦点,则m的值为( )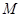 :
: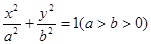 的离心率为
的离心率为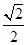 ,点
,点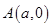 、
、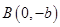 ,原点
,原点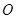 到直线
到直线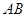 的距离为
的距离为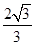 .
.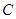
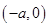 ,点
,点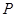 在椭圆
在椭圆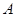 、
、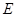 在直线
在直线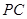 上,若直线
上,若直线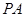 的方程为
的方程为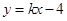 ,且
,且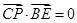 ,试求直线
,试求直线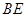 的方程.
的方程. 上的点到直线
上的点到直线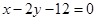 的距离的最小值为 。
的距离的最小值为 。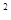 =2x于M(x
=2x于M(x ,y
,y ,y
,y