题目内容
已知抛物线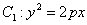 上一点
上一点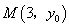 到其焦点
到其焦点 的距离为4;椭圆
的距离为4;椭圆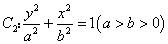 的离心率
的离心率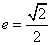 ,且过抛物线的焦点
,且过抛物线的焦点 .
.
(I)求抛物线 和椭圆
和椭圆 的标准方程;
的标准方程;
(II)过点 的直线
的直线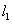 交抛物线
交抛物线 于
于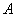 、
、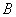 两不同点,交
两不同点,交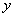 轴于点
轴于点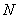 ,已知
,已知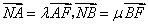 ,求证:
,求证: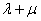 为定值.
为定值.
(III)直线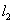 交椭圆
交椭圆 于
于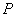 ,
,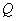 两不同点,
两不同点,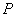 ,
,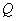 在
在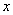 轴的射影分别为
轴的射影分别为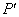 ,
,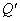 ,
,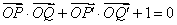 ,若点S满足:
,若点S满足: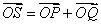 ,证明:点S在椭圆
,证明:点S在椭圆 上.
上.
解析:(Ⅰ)抛物线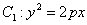 上一点
上一点 到其焦点
到其焦点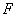 的距离为
的距离为 ;
;
抛物线的准线为
抛物线上点 到其焦点
到其焦点 的距离
的距离 等于到准线的距离
等于到准线的距离
所以 ,所以
,所以
抛物线 的方程为
的方程为
椭圆 的离心率
的离心率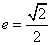 ,且过抛物线的焦点
,且过抛物线的焦点
所以 ,
, ,解得
,解得
所以椭圆的标准方程为
(Ⅱ)直线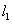 的斜率必存在,设为
的斜率必存在,设为 ,设直线
,设直线 与椭圆
与椭圆 交于
交于
则直线 的方程为
的方程为 ,
, 
联立方程组:
所以
 ,所以
,所以 (*)
(*)
由 得:
得:

得: 
所以
将(*)代入上式,得
(Ⅲ)设
所以 ,则
,则
由 得
得 (1)
(1)
 ,(2)
,(2)  (3)
(3)
(1)+(2)+(3)得:

即 满足椭圆
满足椭圆 的方程
的方程
命题得证

练习册系列答案
相关题目
 ,集合
,集合 ,则下图阴影部分表示的集合是()
,则下图阴影部分表示的集合是() 
 是
是 的重心,
的重心, ,
, ,
, 分别是角
分别是角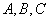 的对边,若
的对边,若 ,则角
,则角 ( )
( ) (B)
(B) (C)
(C) (D)
(D)
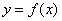 的定义域为
的定义域为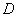 ,如果存在非零常数
,如果存在非零常数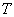 ,对于任意
,对于任意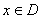 ,都有
,都有 ,则称函数
,则称函数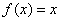 是“似周期函数”;
是“似周期函数”; 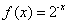 是“似周期函数”;
是“似周期函数”; 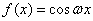 是“似周期函数”,那么“
是“似周期函数”,那么“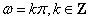 ”.
”.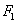 、
、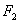 为椭圆
为椭圆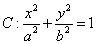 的左、右焦点,
的左、右焦点,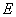 是椭圆的两个顶点,椭圆的离心率
是椭圆的两个顶点,椭圆的离心率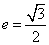 ,
,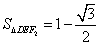 .若
.若 在椭圆
在椭圆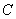 上,则点
上,则点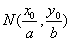 称为点
称为点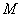 的一个“好点”.直线
的一个“好点”.直线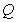 ,已知以
,已知以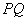 为直径的圆经过坐标原点.
为直径的圆经过坐标原点.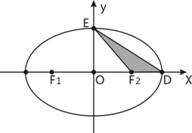
 的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.
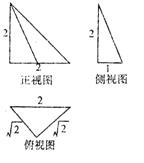
的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由. ,俯视图绕底边所在直线旋转一周形成的几何体的体积记为
,俯视图绕底边所在直线旋转一周形成的几何体的体积记为 ,则
,则 ( )
( )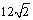 (B)
(B)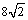 (C)
(C)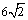 ( D)
( D)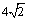
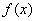 的定义域为D,若存在闭区间
的定义域为D,若存在闭区间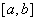
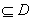 ,使得函数
,使得函数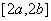 ,则称区间
,则称区间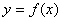 的“和谐区间”。下列函数中存在“和谐区间”的是 .
的“和谐区间”。下列函数中存在“和谐区间”的是 .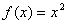 ,
,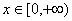 ②
②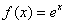 ,
,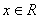
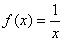 ,
,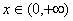 ④
④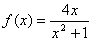 ,
,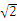 ,则异面直线A1C与B1C1所成的角为
,则异面直线A1C与B1C1所成的角为