题目内容

已知函数f（x）=
1   (x为有理数)
-1    (x为无理数)
，数列an=[f（
2
）n]n，sn是数列{an}的前n项和，则s2013-s2014=
 
．
考点：数列递推式
专题：点列、递归数列与数学归纳法
分析：由数列的前n项和与项的关系得到s2013-s2014=-a2014，然后直接由已知可求得-a2014的值．
解答： 解：由s2013-s2014=-（s2014-s2013）=-a2014．
又f（x）=
1   (x为有理数)
-1    (x为无理数)
，数列an=[f（
2
）n]n，
∴-a2014=-[f(
2
)2014]×2014=-2014．
故答案为：-2014．
点评：本题考查数列递推式，考查了数列的函数特性，的中档题．
练习册系列答案
相关题目
某校高三年级在5月份进行一次质量考试，考生成绩情况如下表所示：
[0，400） [400，480） [480，550） [550，750）
文科考生 67 35 19 6
理科考生 53 x y z
已知用分层抽样方法在不低于550分的考生中随机抽取5名考生进行质量分析，其中文科考生抽取了2名．
（Ⅰ）求z的值；
（Ⅱ）如图是文科不低于550分的6名学生的语文成绩的茎叶图，计算这6名考生的语文成绩的方差；
（Ⅲ）已知该校不低于480分的文科理科考生人数之比为1：2，不低于400分的文科理科考生人数之比为2：5，求x、y的值．
函数f（x）=
log
1
2
(2x-3)
的定义域是
 
．
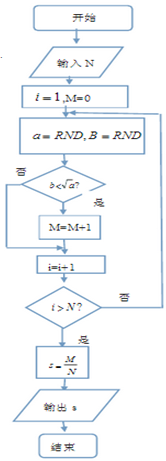在程序中，x=RND表示将计算机产生的[0，1]区间上的均匀随机数赋给变量x．利用如图的程序框图进行随机模拟，我们发现：随着输入N值的增加，输出的S值稳定在某个常数上．这个常数是
 
．（要求给出具体数值）注：框图中的“=”，即为“←”或为“：=”
若角α的终边经过点P（3，2），则tanα的值为
 
．
一个算法的流程图如图所示，则输出y的结果为
 
．
若存在b∈[1，2]，使得2b（b+a）≥4，则实数a的取值范围是
 
．
已知函数f（x）=cosx+
1
2
x，x∈[0，π]，若f（x）在x0处取得极大值，则f（x0）的值为（　　）
A、1
B、
π
4
C、
6
3
+π
12
D、
3+π
6
已知在复平面内，复数z对应的点在第一象限，且满足z2+2
.
z
=2，则复数z的共轭复数
.
z
的虚部为（　　）
A、1B、-iC、-1D、i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网