题目内容
9.已知角α的终边过点P(-8m,-6sin150°),且cosα=-$\frac{4}{5}$,则m的值为( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 由条件利用任意角的三角函数的定义,求出m的值.
解答 解:P(-8m,-3),r=$\sqrt{64{m}^{2}+9}$,
∴cosα=$\frac{-8m}{\sqrt{64{m}^{2}+9}}$=-$\frac{4}{5}$,
∴m>0.
∴$\frac{4{m}^{2}}{64{m}^{2}+9}$=$\frac{1}{25}$,
∴m=±$\frac{1}{2}$.
∵m>0,
∴m=$\frac{1}{2}$.
故选:B.
点评 本题主要考查任意角的三角函数的定义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.执行如图所示的程序框图,若输入t的值为5,则输出的s的值为( )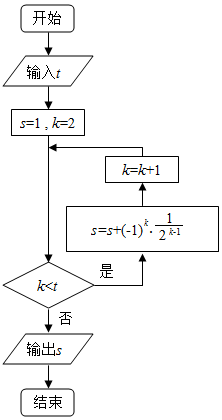

| A. | $\frac{9}{16}$ | B. | $\frac{5}{4}$ | C. | $\frac{21}{16}$ | D. | $\frac{11}{8}$ |
17.角-330°的终边所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.已知角α的终边过点P(-4,-6sin150°),则sin2α的值为( )
| A. | -$\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{12}{25}$ | D. | $\frac{24}{25}$ |
18.已知sin4$\frac{x}{4}$+cos4$\frac{x}{4}$=1,在sin(2016π+x)=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | 0 | C. | -$\frac{\sqrt{2}}{2}$ | D. | -1 |
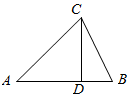 如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°,$\overline{AD}$=λ$\overrightarrow{DB}$
如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°,$\overline{AD}$=λ$\overrightarrow{DB}$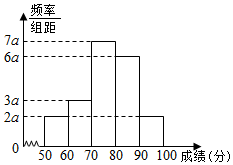 在一次数学竞赛的200名学生考试成绩中利用随机抽样的方法抽取20名学生考试成绩(单位:分)为样本得频率分布直方图如图:
在一次数学竞赛的200名学生考试成绩中利用随机抽样的方法抽取20名学生考试成绩(单位:分)为样本得频率分布直方图如图: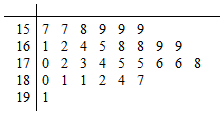 为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”
为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”