题目内容
 如图,四棱锥P-ABCD的底面是边长为2的正方形,且PD⊥底面ABCD,PD=AB,点M的是PC的中点.
如图,四棱锥P-ABCD的底面是边长为2的正方形,且PD⊥底面ABCD,PD=AB,点M的是PC的中点.(1)求证:PA∥平面MBD;
(2)求平面PDC与平面BDM所成锐二面角的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)连结AC,交BD于点O,由已知得MO∥PA,由此能证明PA∥面MBD.
(2)由线面垂直得PD⊥BC,由已知得BC⊥CD,从而BC⊥面PDC,又在Rt△PDC中,DM⊥MC,进而∠BMC为平面PDC与平面BDM所成锐二面角的平面角,由此能求出平面PDC与平面BDM所成锐角二面角的余弦值.
(2)由线面垂直得PD⊥BC,由已知得BC⊥CD,从而BC⊥面PDC,又在Rt△PDC中,DM⊥MC,进而∠BMC为平面PDC与平面BDM所成锐二面角的平面角,由此能求出平面PDC与平面BDM所成锐角二面角的余弦值.
解答:
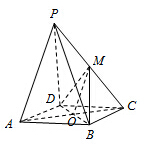 解:(1)证明:连结AC,交BD于点O,
解:(1)证明:连结AC,交BD于点O,
∵四棱锥P-ABCD的底面是边长为2的正方形,
∴O是AC中点,
在△PAC中,点M的是PC的中点,
MO是中位线,∴MO∥PA,
又MO?面MBD,PA?面MBD,∴PA∥面MBD.
(2)解:∵PD⊥面ABCD,∴PD⊥BC,
又BC⊥CD,PD∩CD=D,
∴BC⊥面PDC,又在Rt△PDC中,DM⊥MC,
∴DM⊥MB,∴∠BMC为平面PDC与平面BDM所成锐二面角的平面角,
在Rt△BMC中,∵BC=2,CM=
,BM=
,
∴cos∠BMC=
=
=
,
∴平面PDC与平面BDM所成锐角二面角的余弦值为
.
 解:(1)证明:连结AC,交BD于点O,
解:(1)证明:连结AC,交BD于点O,∵四棱锥P-ABCD的底面是边长为2的正方形,
∴O是AC中点,
在△PAC中,点M的是PC的中点,
MO是中位线,∴MO∥PA,
又MO?面MBD,PA?面MBD,∴PA∥面MBD.
(2)解:∵PD⊥面ABCD,∴PD⊥BC,
又BC⊥CD,PD∩CD=D,
∴BC⊥面PDC,又在Rt△PDC中,DM⊥MC,
∴DM⊥MB,∴∠BMC为平面PDC与平面BDM所成锐二面角的平面角,
在Rt△BMC中,∵BC=2,CM=
| 2 |
| 6 |
∴cos∠BMC=
| MC |
| MB |
| ||
|
| ||
| 3 |
∴平面PDC与平面BDM所成锐角二面角的余弦值为
| ||
| 3 |
点评:本题考查线面平行的证明,考查二面角的余弦值的求法,是中档题,解题题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
已知点 M(x,y)的坐标满足
,N点的坐标为(1,-3),点 O为坐标原点,则
•
的最小值是( )
|
| ON |
| OM |
| A、12 | B、5 | C、-6 | D、-21 |
下列结论中正确的是( )
| A、Z⊆N⊆Q⊆R⊆C |
| B、N⊆Z⊆Q⊆C⊆R |
| C、N⊆Z⊆Q⊆R⊆C |
| D、R⊆N⊆Z⊆Q⊆C |
已知向量
=(m,2),向量
=(2,-3),若
⊥
,则实数m的值是( )
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、3 | ||
C、
| ||
| D、-3 |
已知直线m、n和平面α,则m∥n的必要非充分条件是( )
| A、m、n与α成等角 |
| B、m⊥α且n⊥α |
| C、m∥α且n?α |
| D、m∥α且n∥α |
已知i是虚数单位,若z1=1+i,z2=1-i,(m∈R),则
的虚部为( )
| z1 |
| z2 |
| A、-1 | B、1 | C、i | D、-i |
从正方形的四个顶点及其中心这五个点中,任取两个点,则这两个点的距离不大于该正方形边长的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|