题目内容
某人要制作一个三角形,要求它的三条高的长度分别为
,
,
,则此人能( )
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 7 |
| A、不能作出这样的三角形 |
| B、作出一个锐角三角形 |
| C、作出一个直角三角形 |
| D、作出一个钝角三角形 |
考点:余弦定理
专题:解三角形
分析:先设出三边来,根据面积相等和三条高的长度求得a,b和c的比,进而利用余弦定理求得cosC,通过结果小于0判断出C为钝角.
解答:
解:设三边分别为a,b,c,利用面积相等可知
a=
b=
c,
∴a:b:c=3:5:7,
令a=3,b=5,c=7,
由余弦定理得cosC=
=-
<0,
则角C为钝角,即可作出一个钝角三角形,
故选:D.
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 7 |
∴a:b:c=3:5:7,
令a=3,b=5,c=7,
由余弦定理得cosC=
| 32+52-72 |
| 2×3×5 |
| 1 |
| 2 |
则角C为钝角,即可作出一个钝角三角形,
故选:D.
点评:此题考查了余弦定理,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
如图为一个算法的程序框图,则其输出结果是( )


| A、0 | B、1 |
| C、2013 | D、2014 |
数列{an}满足a1=1,a2=2,an+2=(1+cos2
)an+sin2
,n∈N*,设bn=
,Sn=b1+b2+…+bn,则Sn+
=( )
| nπ |
| 2 |
| nπ |
| 2 |
| a2n-1 |
| a2n |
| n+2 |
| 2n |
| A、0 | ||
| B、2 | ||
| C、1 | ||
D、1+
|
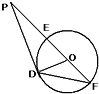 如图,已知P是⊙O外一点,PD为⊙O的切线,D为切点,割线PEF经过圆心O.若PF=16,PD=4
如图,已知P是⊙O外一点,PD为⊙O的切线,D为切点,割线PEF经过圆心O.若PF=16,PD=4| 3 |
| A、13 | B、6.5 | C、7 | D、8 |
已知数列{an}前n项的和Sn=an2+bn(a≠0)是数列{an}成等差数列的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
求值:cos2
-sin2
=( )
| π |
| 12 |
| π |
| 12 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、-
|
已知点(-1,2)和(3,-3)在直线3x+y-a=0的同侧,则a取值范围( )
| A、(-1,6) |
| B、(-6,1) |
| C、(-∞,-1)∪(6,+∞) |
| D、(-∞,-6)∪(1,+∞) |
一元二次不等式(x-1)(x-3)<0的解集是( )
| A、(-∞,1) |
| B、(1,3) |
| C、(3,+∞) |
| D、(-∞,1)∪(3,+∞) |