题目内容
16.设函数f(x)=|x-a|.(1)当a=2时,求不等式f(x)≤4+|2x-1|的解集;
(2)若A={x|x2-4x≤0},关于x的不等式f(x)≤a2-2的解集为B,且B⊆A,求实数a的取值范围.
分析 (1)方法一:将a=2代入f(x),问题转化为解不等式|x-2|-|2x-1|-4≤0即可;方法二:令g(x)=|x-2|-|2x-1|-4,结合函数的单调性求出不等式的解集即可;
(2)通过讨论a的范围结合集合的包含关系,从而求出a的范围即可.
解答 解:(1)解法1:a=2时,f(x)≤4+|2x-1|即为|x-2|-|2x-1|-4≤0可化为:
$\left\{\begin{array}{l}x<\frac{1}{2}\\ x-3≤0\end{array}\right.或\left\{\begin{array}{l}\frac{1}{2}≤x≤2\\-3x-1≤0\end{array}\right.或\left\{\begin{array}{l}x>2\\-x-5≤0\end{array}\right.$…(3分)
解得$x<\frac{1}{2}或\frac{1}{2}≤x≤2或x>2$…(4分)
所以不等式f(x)≤4+|2x-1|的解集为R.…5 分
解法2:令g(x)=|x-2|-|2x-1|-4,
则 $g(x)=\left\{\begin{array}{l}x-3,x<\frac{1}{2}\\-3x-1,\frac{1}{2}≤x≤2\\-x-5,x>2\end{array}\right.$…(3分),
$当x<\frac{1}{2}时,g(x)单调递增,当x≥\frac{1}{2}时,g(x)单调递减$,
所以$g(x)≤g(\frac{1}{2})=-2<0$…(4分)
所以不等式f(x)≤4+|2x-1|的解集为R.…(5分)
(2)A={x|x(x-4)≤0}={x|0≤x≤4}…(6分)
①$-\sqrt{2}<a<\sqrt{2}$时a2-2<0,这时f(x)≤a2-2的解集为φ,
满足B⊆A,所以$-\sqrt{2}<a<\sqrt{2}$…(7分)
②当$a≤-\sqrt{2}或a≥\sqrt{2}$时a2-2≥0,B≠φ
这时f(x)≤a2-2即|x-a|≤a2-2可化为2+a-a2≤x≤a2+a-2
所以B={x|2+a-a2≤x≤a2+a-2}…(8分)
因为B⊆A
所以$\left\{\begin{array}{l}{a^2}+a-2≤4\\ 2+a-{a^2}≥0\end{array}\right.$即$\left\{\begin{array}{l}{a^2}+a-6≤0\\{a^2}-a-2≤0\end{array}\right.$即$\left\{\begin{array}{l}({a-2})({a+3})≤0\\({a-2})({a+1})≤0\end{array}\right.$
所以-1≤a≤2…(9分)
又因为$a≤-\sqrt{2}或a≥\sqrt{2}$所以$\sqrt{2}≤a≤2$
综合①②得实数a的取值范围为$(-\sqrt{2},2]$…(10分)
点评 本题考察了解绝对值不等式问题,考察集合问题,分类讨论思想,是一道中档题.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案| A. | $\frac{n}{{2}^{n}}$ | B. | n•2n-1 | C. | n•2n | D. | $\frac{n}{{2}^{n-1}}$ |

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
| A. | 1+i | B. | 1-i | C. | 2+2i | D. | 2-2i |
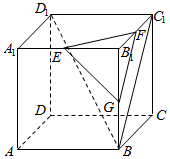 在正方体ABCD-A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,给出下列四个推断:
在正方体ABCD-A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,给出下列四个推断:①FG∥平面AA1D1D; ②EF∥平面BC1D1;
③FG∥平面BC1D1; ④平面EFG∥平面BC1D1
其中推断正确的序号是( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
| A. | $(0,\frac{1}{2})$ | B. | $(0,\frac{2}{{3\sqrt{e}}})$ | C. | $(-∞,\frac{1}{2}]$ | D. | $(-∞,\frac{2}{{3\sqrt{e}}}]$ |
| A. | 1 | B. | -1 | C. | 0 | D. | 与a有关 |
| A. | 周期为π的奇函数 | B. | 周期为π的偶函数 | ||
| C. | 周期为2π的奇函数 | D. | 周期为2π的偶函数 |