МвДїДЪИЭ
ЎѕМвДїЎї№ЕИЛФЖЈєЎ°ё№УРК«КйЖшЧФ»Є.Ў±ОЄПмУ¦И«ГсФД¶БЈ¬ЅЁЙиКйПгЦР№ъЈ¬РЈФ°¶БКй»о¶ЇµДИИі±ХэФЪРЛЖр.ДіРЈОЄНіјЖС§ЙъТ»ЦЬїОНв¶БКйµДК±јдЈ¬ґУИ«РЈС§ЙъЦРЛж»ъійИЎ![]() ГыС§ЙъЅшРРОКѕнµч–ЛЈ¬НіјЖБЛЛыГЗТ»ЦЬїОНв¶БКйК±јдЈЁµҐО»Јє
ГыС§ЙъЅшРРОКѕнµч–ЛЈ¬НіјЖБЛЛыГЗТ»ЦЬїОНв¶БКйК±јдЈЁµҐО»Јє![]() Ј©µДКэѕЭИзПВЈє
Ј©µДКэѕЭИзПВЈє
Т»ЦЬїОНв¶БКйК±јд/ |
|
|
|
|
|
|
|
|
| єПјЖ |
ЖµКэ | 4 | 6 | 10 | 12 | 14 | 24 |
| 46 | 34 |
|
ЖµВК | 0.02 | 0.03 | 0.05 | 0.06 | 0.07 | 0.12 | 0.25 |
| 0.17 | 1 |
ЈЁ1Ј©ёщѕЭ±нёсЦРМṩµДКэѕЭЈ¬Зу![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() µДЦµІў№АЛгТ»ЦЬїОНв¶БКйК±јдµДЦРО»Кэ.
µДЦµІў№АЛгТ»ЦЬїОНв¶БКйК±јдµДЦРО»Кэ.
ЈЁ2Ј©Из№ы¶БКйК±јд°ґ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ·ЦЧйЈ¬УГ·ЦІгійСщµД·Ѕ·ЁґУ
·ЦЧйЈ¬УГ·ЦІгійСщµД·Ѕ·ЁґУ![]() ГыС§ЙъЦРійИЎ20ИЛ.
ГыС§ЙъЦРійИЎ20ИЛ.
ўЩЗуГїІгУ¦ійИЎµДИЛКэЈ»
ўЪИфґУ![]() Ј¬
Ј¬![]() ЦРійіцµДС§ЙъЦРФЩЛж»ъСЎИЎ2ИЛЈ¬ЗуХв2ИЛІ»ФЪН¬Т»ІгµДёЕВК.
ЦРійіцµДС§ЙъЦРФЩЛж»ъСЎИЎ2ИЛЈ¬ЗуХв2ИЛІ»ФЪН¬Т»ІгµДёЕВК.
Ўѕґр°ёЎїЈЁ1Ј©![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ЦРО»Кэ
Ј¬ЦРО»Кэ![]() Ј»ЈЁ2Ј©ўЩИэІгЦРійИЎµДИЛКэ·Ц±рОЄ2Ј¬5Ј¬13Ј»ўЪ
Ј»ЈЁ2Ј©ўЩИэІгЦРійИЎµДИЛКэ·Ц±рОЄ2Ј¬5Ј¬13Ј»ўЪ![]()
ЎѕЅвОцЎї
ЈЁ1Ј©ёщѕЭЖµВК·ЦІјЦ±·Ѕ±нµДРФЦКЈ¬јґїЙЗуµГ![]() Ј¬µГµЅ
Ј¬µГµЅ![]() Ј¬
Ј¬![]() Ј¬ФЩЅбєПЦРО»КэµДјЖЛг·Ѕ·ЁЈ¬јґїЙЗуЅв.
Ј¬ФЩЅбєПЦРО»КэµДјЖЛг·Ѕ·ЁЈ¬јґїЙЗуЅв.
ЈЁ2Ј©ўЩУЙМвТвЦЄУГ·ЦІгійСщµД·Ѕ·ЁґУСщ±ѕЦРійИЎ20ИЛЈ¬ёщѕЭійСщ±ИЈ¬ЗуµГФЪИэІгЦРійИЎµДИЛКэЈ»
ўЪУЙўЩЦЄЈ¬Йи![]() ДЪ±»ійИЎµДС§Йъ·Ц±рОЄ
ДЪ±»ійИЎµДС§Йъ·Ц±рОЄ![]() Ј¬
Ј¬![]() ДЪ±»ійИЎµДС§Йъ·Ц±рОЄ
ДЪ±»ійИЎµДС§Йъ·Ц±рОЄ![]() Ј¬АыУГБРѕЩ·ЁµГµЅ»щ±ѕКВјюµДЧЬКэЈ¬АыУГ№ЕµдёЕРНµДёЕВКјЖЛ㹫ʽЈ¬јґїЙЗуЅв.
Ј¬АыУГБРѕЩ·ЁµГµЅ»щ±ѕКВјюµДЧЬКэЈ¬АыУГ№ЕµдёЕРНµДёЕВКјЖЛ㹫ʽЈ¬јґїЙЗуЅв.
ЈЁ1Ј©УЙМвТвЈ¬їЙµГ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() Ј¬
Ј¬![]() .
.
ЙиТ»ЦЬїОНв¶БКйК±јдµДЦРО»КэОЄ![]() РЎК±Ј¬
РЎК±Ј¬
Фт![]() Ј¬ЅвµГ
Ј¬ЅвµГ![]() Ј¬
Ј¬
јґТ»ЦЬїОНв¶БКйК±јдµДЦРО»КэФјОЄ![]() РЎК±.
РЎК±.
ЈЁ2Ј©ўЩУЙМвТвЦЄУГ·ЦІгійСщµД·Ѕ·ЁґУСщ±ѕЦРійИЎ20ИЛЈ¬ійСщ±ИОЄ![]() Ј¬
Ј¬
УЦТтОЄ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() µДЖµКэ·Ц±рОЄ20Ј¬50Ј¬130Ј¬
µДЖµКэ·Ц±рОЄ20Ј¬50Ј¬130Ј¬
ЛщТФґУ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ИэІгЦРійИЎµДИЛКэ·Ц±рОЄ2Ј¬5Ј¬13.
ИэІгЦРійИЎµДИЛКэ·Ц±рОЄ2Ј¬5Ј¬13.
ўЪУЙўЩЦЄЈ¬ФЪ![]() Ј¬
Ј¬![]() БЅІгЦР№ІійИЎ7ИЛЈ¬Йи
БЅІгЦР№ІійИЎ7ИЛЈ¬Йи![]() ДЪ±»ійИЎµДС§Йъ·Ц±рОЄ
ДЪ±»ійИЎµДС§Йъ·Ц±рОЄ![]() Ј¬
Ј¬![]() ДЪ±»ійИЎµДС§Йъ·Ц±рОЄ
ДЪ±»ійИЎµДС§Йъ·Ц±рОЄ![]() Ј¬
Ј¬
ИфґУХв7ИЛЦРЛж»ъійИЎ2ИЛЈ¬ФтЛщУРЗйїцОЄ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬№ІУР21ЦЦЈ¬
Ј¬№ІУР21ЦЦЈ¬
ЖдЦР2ИЛІ»ФЪН¬Т»ІгµДЗйїцОЄ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬№ІУР10ЦЦ.
Ј¬№ІУР10ЦЦ.
ЙиКВјю![]() ОЄЎ°Хв2ИЛІ»ФЪН¬Т»ІгЎ±Ј¬
ОЄЎ°Хв2ИЛІ»ФЪН¬Т»ІгЎ±Ј¬
УЙ№ЕµдёЕРНµДёЕВКјЖЛ㹫ʽЈ¬їЙµГёЕВКОЄ![]() .
.

 ЦЗИ¤КојЩОВ№КЦЄРВПµБРґр°ё
ЦЗИ¤КојЩОВ№КЦЄРВПµБРґр°ё УўУпРЎУўРЫМмМмД¬РґПµБРґр°ё
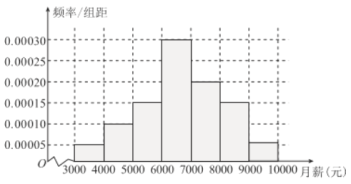
УўУпРЎУўРЫМмМмД¬РґПµБРґр°ёЎѕМвДїЎї2019ДкЈ¬єЈДПµИ8КЎ№«ІјБЛёЯїјёДёпЧЫєП·Ѕ°ёЅ«ІЙИЎЎ°![]() Ў±ДЈКЅЈ¬јґУпОДЎўКэС§ЎўУўУп±ШїјЈ¬И»єуїјЙъПИФЪОпАнЎўАъК·ЦРСЎФс1ГЕЈ¬ФЩФЪЛјПлХюЦОЎўµШАнЎў»ЇС§ЎўЙъОпЦРСЎФс2ГЕОЄБЛёьєГЅшРРЙъСД№ж»®Ј¬јЧН¬С§¶ФёЯТ»Т»ДкАґµДЖЯґОїјКФіЙјЁЅшРРНіјЖ·ЦОцЈ¬ЖдЦРОпАнЎўАъК·іЙјЁµДѕҐТ¶НјИзНјЛщКѕ.
Ў±ДЈКЅЈ¬јґУпОДЎўКэС§ЎўУўУп±ШїјЈ¬И»єуїјЙъПИФЪОпАнЎўАъК·ЦРСЎФс1ГЕЈ¬ФЩФЪЛјПлХюЦОЎўµШАнЎў»ЇС§ЎўЙъОпЦРСЎФс2ГЕОЄБЛёьєГЅшРРЙъСД№ж»®Ј¬јЧН¬С§¶ФёЯТ»Т»ДкАґµДЖЯґОїјКФіЙјЁЅшРРНіјЖ·ЦОцЈ¬ЖдЦРОпАнЎўАъК·іЙјЁµДѕҐТ¶НјИзНјЛщКѕ.
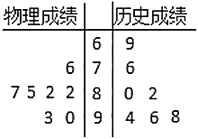
ЈЁ1Ј©ИфјЧН¬С§Лж»ъСЎФс3ГЕ№¦їОЈ¬ЗуЛыСЎµЅОпАнЎўµШАнБЅГЕ№¦їОµДёЕВКЈ»
ЈЁ2Ј©КФёщѕЭѕҐТ¶Нј·ЦОцјЧН¬С§µДОпАнєНАъК·ДДТ»С§їЖіЙјЁёьОИ¶Ё.ЈЁІ»РијЖЛгЈ©
ЈЁ3Ј©јЧН¬С§·ўПЦЈ¬ЖдОпАнїјКФіЙјЁ![]() ЈЁ·ЦЈ©Ул°ај¶ЖЅѕщ·Ц
ЈЁ·ЦЈ©Ул°ај¶ЖЅѕщ·Ц![]() ЈЁ·ЦЈ©ѕЯУРПЯРФПа№Ш№ШПµЈ¬НіјЖКэѕЭИзПВ±нЛщКѕЈ¬КФЗуµ±°ај¶ЖЅѕщ·ЦОЄ50·ЦК±Ј¬ЖдОпАнїјКФіЙјЁ.ЈЁјЖЛг
ЈЁ·ЦЈ©ѕЯУРПЯРФПа№Ш№ШПµЈ¬НіјЖКэѕЭИзПВ±нЛщКѕЈ¬КФЗуµ±°ај¶ЖЅѕщ·ЦОЄ50·ЦК±Ј¬ЖдОпАнїјКФіЙјЁ.ЈЁјЖЛг![]() Ј¬
Ј¬![]() К±ѕ«И·µЅ0.01Ј©
К±ѕ«И·µЅ0.01Ј©
| 57 | 61 | 65 | 72 | 74 | 77 | 84 |
| 76 | 82 | 82 | 85 | 87 | 90 | 93 |
ІОїјКэѕЭЈє![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() .
.
ІОїј№«КЅЈє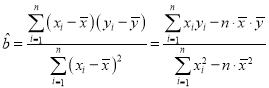 Ј¬
Ј¬![]()