Question

【题目】已知平面，，，分别为，上的点，且，.

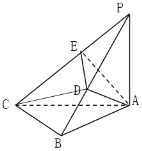
（1）求证：；

（2）若，直线与平面所成角的正弦值为，求二面角的余弦值.

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

（1）先证明BC⊥平面PAB，可得BC⊥AD，证明AD⊥平面PBC，得PC⊥AD，再证明PC⊥平面ADE，即可证明PC⊥DE；

（2）过点B作BE∥AP，则BZ⊥平面ABC，分别以BA，BC，BZ所在直线为x轴，y轴，z轴建立空间直角坐标系，设，根据PC⊥平面ADE，可得是平面ADE的一个法向量，从而向量与所成的角的余弦值的绝对值为，可求PA的值，利用题目条件求出平面的一个法向量，利用夹角公式可得二面角的余弦值.

（1）证明：因为平面，∴，

又，，

∴平面，∴.

又，，

∴平面，∴.

又，，

∴平面，∴.

（2）过点作，则平面，如图所示

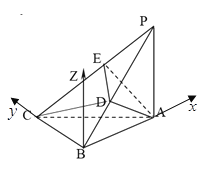
分别以，，所在直线为轴，轴，轴建立空间直角坐标系.

设，则，，，

因为平面，

∴是平面的一个法向量，

∴向量与所成的角的余弦值的绝对值为，

又，

，

∴，∴.

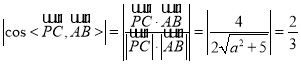在中，，又，

∴为中点，∴，

∴，，

设平面的一个法向量为，

则，∴，∴，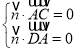

又是平面的法向量，

∴，，

二面角的余弦值为.