题目内容
已知数列 满足
满足 ,
, ,
, ,且
,且 是等比数列。
是等比数列。
(Ⅰ)求 的值;
的值;
(Ⅱ)求出通项公式 ;
;
(Ⅲ)求证: …
…
(Ⅰ) ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
解析试题分析:(Ⅰ) ,这是已知
,这是已知 型求
型求 ,可利用
,可利用 ,来求出递推式,得
,来求出递推式,得 ,由
,由 得数列
得数列 得公比为
得公比为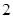 ,由
,由 ,求出
,求出 ,则
,则 ,从而可求出
,从而可求出 ;(Ⅱ)求出通项公式
;(Ⅱ)求出通项公式 ,由(Ⅰ)知数列
,由(Ⅰ)知数列 是以
是以 为首项,2为公比的等比数列,这样能写出
为首项,2为公比的等比数列,这样能写出 的通项公式,从而可得数列
的通项公式,从而可得数列 的通项公式
的通项公式 ;(Ⅲ)求证:
;(Ⅲ)求证: …
… ,观察式子,当
,观察式子,当 时,
时,
 ,这样相邻两项相加,相邻两项相加,得到一个等比数列,利用等比数列的前n项和公式,即可证得.
,这样相邻两项相加,相邻两项相加,得到一个等比数列,利用等比数列的前n项和公式,即可证得.
试题解析:(1)当 时,
时,



又
 又
又

 5分
5分
(Ⅱ)由(1)知 是以
是以 为首项,2为公比的等比数列
为首项,2为公比的等比数列 ,
, 7分
7分
(Ⅲ)当 时,
时,
 10分
10分
将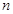 由2到
由2到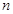 赋值并累加得:
赋值并累加得: …
… …
…
 13分
13分
考点:数列的通项公式,数列求和.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 满足
满足 (
( ).
). 的值;
的值; (用含
(用含 的式子表示);
的式子表示); ,求
,求 为
为 阶“期待数列”:
阶“期待数列”: ;②
;② .
. 为
为 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及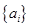 的前k项和为
的前k项和为 :
: ;
; 使
使 ,试问数列
,试问数列 能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.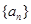 的前
的前 项和为
项和为 ,若
,若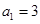 ,点
,点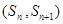 在直线
在直线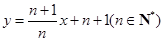 上.
上.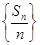 是等差数列;
是等差数列;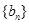 满足
满足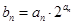 ,求数列
,求数列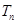 ;
;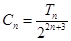 ,求证:
,求证: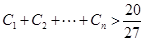 .
.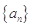 的前n项和为
的前n项和为 ,已知
,已知 ,
, 是
是 和
和 的等比中项.
的等比中项.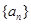 的前
的前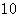 项和
项和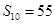 ,且
,且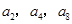 成等比数列.
成等比数列.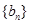 满足
满足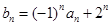 ,求
,求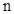 项和
项和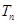 .
. 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 ,都有
,都有 (
( 为正常数).
为正常数). 满足
满足 ,
, ,求数列
,求数列 的前
的前 .
. 满足
满足 ,
,
 ,求数列
,求数列 的前
的前 项和
项和 .
. 的前
的前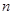 项和为
项和为
 ,对于任意的
,对于任意的 恒有
恒有

 的通项公式
的通项公式
 证明:
证明: