题目内容
数列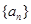 的前
的前 项和为
项和为 ,若
,若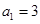 ,点
,点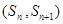 在直线
在直线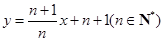 上.
上.
⑴求证:数列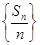 是等差数列;
是等差数列;
⑵若数列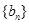 满足
满足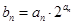 ,求数列
,求数列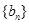 的前
的前 项和
项和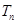 ;
;
⑶设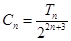 ,求证:
,求证: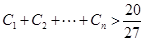 .
.
(1)证明过程详见解析;(2)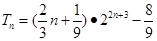 ;(3)证明过程详见解析.
;(3)证明过程详见解析.
解析试题分析:本题考查等比数列、等差数列、不等式等基础知识,考查运算能力、推理论证能力.第一问,由于点在直线上,所以将点代入得到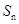 与
与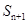 的关系式,两边同除以
的关系式,两边同除以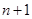 ,凑出新的等差数列,并求出首项个公差;第二问,先利用第一问的结论求出
,凑出新的等差数列,并求出首项个公差;第二问,先利用第一问的结论求出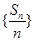 的通项公式,得到
的通项公式,得到 的表达式,由
的表达式,由 求
求 ,将得到的结论代入到
,将得到的结论代入到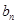 中,用错位相减法求
中,用错位相减法求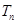 ,在解题过程中用到了等比数列的前n项公式;第三问,先将第二问的结论代入,利用分组求和的方法先求出
,在解题过程中用到了等比数列的前n项公式;第三问,先将第二问的结论代入,利用分组求和的方法先求出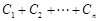 ,当
,当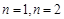 时,具体比较结果与
时,具体比较结果与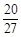 的大小,当
的大小,当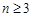 时,得到的数都比
时,得到的数都比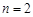 的结果大,所以都大于
的结果大,所以都大于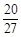 ,所以不等式成立.
,所以不等式成立.
试题解析:(1)∵点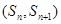 在直线
在直线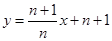 (
(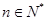 )上,
)上,
∴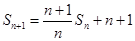 ,
,
两边同除以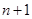 ,得
,得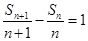 ,
,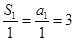 ,
,
于是,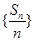 是以3为首项,1为公差的等差数列.
是以3为首项,1为公差的等差数列.
(2)∵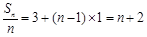 ,∴
,∴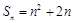 ,
,
∴当 时,
时,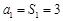 ,
,
当 时,
时,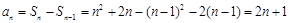 ,
,
∴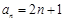
∴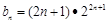 ,
,
∴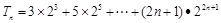
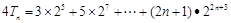
∴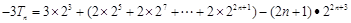

∴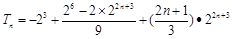
∴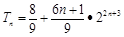 .
.
(3)∵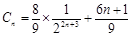 ,
,
∴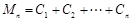
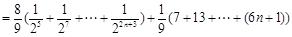
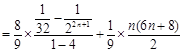
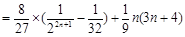
当 时,
时,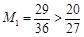 ,
,
当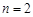 时,
时,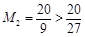 ,
,
当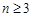 时,
时,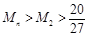 ,
,
所以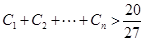 .
.
考点:1.配凑法求通项公式;2.等差数列的通项公式;3.错位相减法;4.等比数列的前n项和公式;5.分组求和.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 千元时多卖出
千元时多卖出 件。
件。 与n的函数关系式;
与n的函数关系式; 时,厂家应该生产多少件产品,做几千元的广告,才能获利最大?
时,厂家应该生产多少件产品,做几千元的广告,才能获利最大?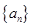 ,其前n项和
,其前n项和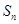 满足
满足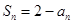 ;等差数列
;等差数列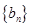 中
中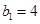 ,且
,且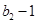 是
是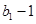 与
与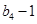 的等比中项
的等比中项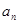 和
和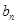 ,
,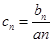 ,求
,求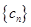 的前n项和
的前n项和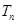 .
.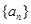 的各项均为正数,其前n项的和为
的各项均为正数,其前n项的和为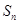 ,对于任意正整数m,n,
,对于任意正整数m,n, 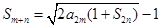 恒成立.
恒成立. 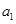 =1,求
=1,求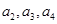 及数列
及数列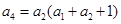 ,求证:数列
,求证:数列 的前
的前 项和
项和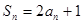 ,求证:
,求证: }中,a1=1,
}中,a1=1, 是数列{
是数列{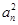 +p
+p 满足
满足 ,
, ,
, ,且
,且 是等比数列。
是等比数列。 的值;
的值; ;
; …
…
 为公差不为
为公差不为 的等差数列,
的等差数列, 为前
为前 项和,
项和, 和
和 的等差中项为
的等差中项为 ,且
,且 .令
.令 数列
数列 的前
的前 .
. 及
及 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.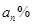 ,B喷雾器中药水的浓度为
,B喷雾器中药水的浓度为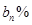 .
.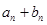 是一个常数;
是一个常数; 与
与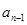 的关系式;
的关系式;