题目内容
称满足以下两个条件的有穷数列 为
为 阶“期待数列”:
阶“期待数列”:
① ;②
;② .
.
(1)若等比数列 为
为 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及 的通项公式;
的通项公式;
(2)若一个等差数列 既是
既是 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记n阶“期待数列”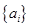 的前k项和为
的前k项和为 :
:
(i)求证: ;
;
(ii)若存在 使
使 ,试问数列
,试问数列 能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
(1)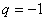 .
.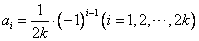 或
或 ;
;
(2)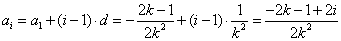 ;
;
(3)(i)证明见解析;(ii)不能,证明见解析.
解析试题分析:(1)数列 中等比数列,因此
中等比数列,因此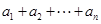 是其前
是其前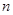 和,故利用前前
和,故利用前前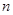 项和公式,分
项和公式,分 和
和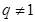 进行讨论,可很快求出
进行讨论,可很快求出 ,
, 或
或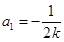 ;(2)
;(2) 阶等差数列是递增数列,即公差
阶等差数列是递增数列,即公差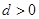 ,其和为0,故易知数列前面的项为负,后面的项为正,即前
,其和为0,故易知数列前面的项为负,后面的项为正,即前 项为正,后
项为正,后 项为正,因此有
项为正,因此有 ,
,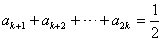 ,这两式用基本量或直接相减可求得
,这两式用基本量或直接相减可求得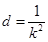 ,
,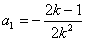 ,因此通项公式可得;(3)(i)我们只要把数列中所有非负数项的和记为
,因此通项公式可得;(3)(i)我们只要把数列中所有非负数项的和记为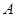 ,所有负数项的记为
,所有负数项的记为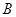 ,则
,则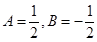 ,
,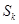 不可能比
不可能比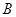 小,同样
小,同样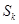 不可能比
不可能比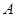 大,即
大,即 ,得证;(ii)若
,得证;(ii)若 ,则一定有
,则一定有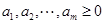 ,
,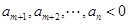 ,且
,且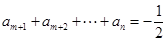 ,若数列
,若数列 为n阶“期待数列”,设其前
为n阶“期待数列”,设其前 项和为
项和为 ,首先
,首先 ,而
,而 ,
,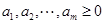 ,因此
,因此 ,即
,即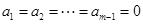 ,
, ,从而
,从而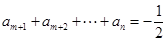 ,于是
,于是 ,那么
,那么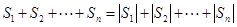 ,矛盾出现了,故结论是否定的.
,矛盾出现了,故结论是否定的.
试题解析:(1)①若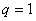 ,由①得,
,由①得,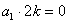 ,得
,得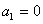 ,矛盾. 1分
,矛盾. 1分
若 ,则由①
,则由①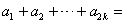
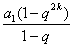 =0,得
=0,得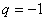 , 3分
, 3分
由②得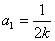 或
或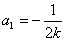 .
.
所以,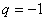 .数列
.数列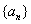 的通项公式是
的通项公式是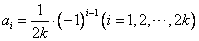
或 4分
4分
(2)设等差数列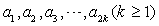 的公差为
的公差为 ,
, >0.
>0.
∵ ,∴
,∴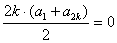 ,∴
,∴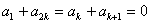 ,
,
∵ >0,由
>0,由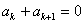 得
得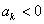 ,
,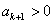 ,
,
由①、②得 ,
,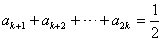 , 6分
, 6分
两式相减得,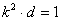 , ∴
, ∴ ,
,
又 ,得
,得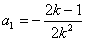 ,
,
∴数列
练习册系列答案
相关题目
 中各项均为正,有
中各项均为正,有 ,
, ,
, 中,
中, ,点
,点 在直线
在直线 上.
上. 和
和 的值;(2)求数列
的值;(2)求数列 和
和 ;
; ,求数列
,求数列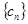 的前n项和
的前n项和 .
.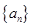 ,其前n项和
,其前n项和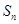 满足
满足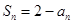 ;等差数列
;等差数列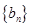 中
中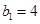 ,且
,且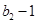 是
是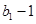 与
与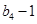 的等比中项
的等比中项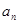 和
和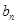 ,
,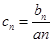 ,求
,求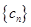 的前n项和
的前n项和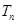 .
. 中满足
中满足 ,
, .
. 和公差
和公差 ;
;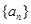 的各项均为正数,其前n项的和为
的各项均为正数,其前n项的和为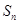 ,对于任意正整数m,n,
,对于任意正整数m,n, 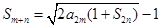 恒成立.
恒成立. 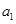 =1,求
=1,求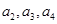 及数列
及数列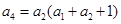 ,求证:数列
,求证:数列 的前
的前 项和
项和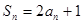 ,求证:
,求证: 满足
满足 ,
, ,
, ,且
,且 是等比数列。
是等比数列。 的值;
的值; ;
; …
…
 }中,
}中, ,又
,又 成等比数列.
成等比数列. ,求数列{
,求数列{ }的前n项和
}的前n项和 .
.