题目内容
1. 某校从参加高三年级期末考试的学生中随机抽取100名学生,将其数学成绩分成五段:[50,70),[70,90),[90,110),[110,130),[130,150],它的频率分布直方图如图所示,则该批学生中成绩不低于90分的人数是65.
某校从参加高三年级期末考试的学生中随机抽取100名学生,将其数学成绩分成五段:[50,70),[70,90),[90,110),[110,130),[130,150],它的频率分布直方图如图所示,则该批学生中成绩不低于90分的人数是65.
分析 根据频率分布直方图,结合频率、频数与样本容量的关系,求出对应的人数即可.
解答 解:根据频率分布直方图,得;
该批学生中成绩低于90分的频率是
(0.0025+0.0150)×20=0.35,
∴该批学生中成绩不低于90分的频率是
1-0.35=0.65,
∴该批学生中成绩不低于90分的人数是
100×0.65=65.
故答案为:65.
点评 本题考查了频率分布直方图的应用问题,也考查了频率=$\frac{频数}{样本容量}$的应用问题,是基础题目.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
9.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右顶点分别为A,B,左右焦点分别为F1,F2,点O为坐标原点,线段OB的中垂线与椭圆在第一象限的交点为P,设直线PA,PB,PF1,PF2的斜率分别为k1,k2,k3,k4,若k1•k2=-$\frac{1}{4}$,则k3•k4=( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{8}{3}$ | C. | $-\frac{3}{8}$ | D. | -4 |
16.已知i为虚数单位,a∈R,若a2-1+(a+1)i为纯虚数,则复数z=a+(a-2)i 在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.设点P在曲线y=ex,点Q在曲线y=lnx上,则|PQ|最小值为( )
| A. | ln2 | B. | $\sqrt{2}$ | C. | 1+$\sqrt{2}$ | D. | $\sqrt{2}$-1 |
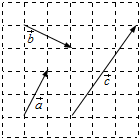 如图,在6×6的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,(x,y∈R),则x+y=( )
如图,在6×6的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,(x,y∈R),则x+y=( )