题目内容
已知函数f（x）=2sin（x+φ），且f（0）=1，f'（0）＜0，则函数y=f(x-
)图象的一条对称轴的方程为（ ）
| π |
| 3 |
| A、x=0 | ||
B、x=
| ||
C、x=
| ||
D、x=
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由题意可得 2sinφ=1，且2cosφ＜0，可取φ=
，可得函数f（x）的解析式，从而得到函数y=f(x-
) 的解析式，再根据z余弦函数的图象的对称性得出结论．
| 5π |
| 6 |
| π |
| 3 |
解答：
解：∵函数f（x）=2sin（x+φ），且f（0）=1，f'（0）＜0，∴2sinφ=1，且2cosφ＜0，
∴可取φ=
，函数f（x）=2sin（x+
）．
∴函数y=f(x-
)=2sin（x+
）=2cosx，故函数y=f(x-
)图象的对称轴的方程为x=kπ，k∈z．
结合所给的选项，
故选：A．
∴可取φ=
| 5π |
| 6 |
| 5π |
| 6 |
∴函数y=f(x-
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
结合所给的选项，
故选：A．
点评：本题主要考查三角函数的导数，余弦函数的图象的对称性，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
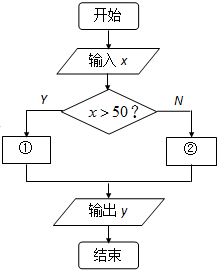某铁路客运部门规定甲、乙两地之间旅客托运行李的费用为：不超过50kg按0.53元/kg收费，超过50kg的部分按0.85元/kg收费．相应收费系统的流程图如右图所示，则①处应填（ ）| A、y=0.85x |
| B、y=0.53x |
| C、y=50×0.53+（x-50）×0.85 |
| D、y=50×0.53+0.85x |
若在区间[0，2]中随机地取两个数，则这两个数中较小的数大于
的概率是（ ）
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知全集U={x∈N*|x＜6}，A={1，3}，B={3，5}，则∁U（A∪B）等于（ ）
| A、{1，4} |
| B、{1，5} |
| C、{2，4} |
| D、{2，5} |
设z1，z2为复数，则下列四个结论中正确的是（ ）
| A、若z12+z22＞0，则z12＞-z22 | ||
| B、若z12+z22=0，则z1=z2=0 | ||
C、|z1-z2|=
| ||
D、z1-
|
设全集U=R，集合A={x|x＜0}，B={x|-1＜x＜3}，则A∩B=（ ）
| A、{x|-1＜x＜0} |
| B、{x|0＜x＜3} |
| C、{x|x＜0} |
| D、{x|x＜3} |