题目内容
14．已知函数f（x）=xcos2x，则f′（x）=cos2x-2xsin2x，曲线y=f（x）在点（$\frac{π}{2}$，-$\frac{π}{2}$）处的切线倾斜角是135°．分析 根据导数的运算法则和导数的几何意义即可求出．
解答 解：f′（x）=x′cos2x+x（cos2x）′=cos2x-2xsin2x，
k=f′（$\frac{π}{2}$）=cosπ=-1=tanθ
∴θ=135°
故答案为：cos2x-2xsin2x，135°．
点评 本题考查了导数的运算法则和导数的几何意义，属于基础题．
练习册系列答案
相关题目
4．下列函数中，既是偶函数又在（0，+∞）单调递增的函数是（ ）
| A． | y=x3 | B． | y=|x|+1 | C． | y=-x2+1 | D． | y=2x |
9．
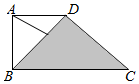如图，在直角梯形ABCD中，DA=AB=1，BC=2，点P在阴影区域（含边界）中运动，则有$\overrightarrow{AP}•\overrightarrow{BD}$的取值范围是（ ）
如图，在直角梯形ABCD中，DA=AB=1，BC=2，点P在阴影区域（含边界）中运动，则有$\overrightarrow{AP}•\overrightarrow{BD}$的取值范围是（ ）| A． | [-1，1] | B． | $[{-1，\frac{1}{2}}]$ | C． | $[{-\frac{1}{2}，1}]$ | D． | [-1，0] |
19．为了得到函数$y=sin（2x+\frac{π}{3}）$的图象，可将函数y=sin2x的图象向左平移m个单位长度或向右平移n个单位长度（m，n均为正数），则|m-n|的最小值是（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{4π}{3}$ | D． | $\frac{5π}{3}$ |