题目内容
4.已知f(x)=x3-$\frac{1}{2}$x2-2x+a,对任意x∈[-1,2]有f(x)<3a2,求a的取值范围.分析 f(x)<3a2,x3-$\frac{1}{2}$x2-2x+a<3a2,化为:x3-$\frac{1}{2}$x2-2x<3a2-a.对任意x∈[-1,2]有f(x)<3a2,可得3a2-a>$({x}^{3}-\frac{1}{2}{x}^{2}-2x)_{max}$,利用导数研究函数的单调性极值与最值即可得出.
解答 解:f(x)<3a2,x3-$\frac{1}{2}$x2-2x+a<3a2,化为:x3-$\frac{1}{2}$x2-2x<3a2-a,
∵对任意x∈[-1,2]有f(x)<3a2,
∴3a2-a>$({x}^{3}-\frac{1}{2}{x}^{2}-2x)_{max}$,
令g(x)=x3-$\frac{1}{2}$x2-2x,x∈[-1,2].
∴g′(x)=3x2-x-2=(3x+2)(x-1),
当x∈$[-1,-\frac{2}{3})$时,g′(x)>0,此时函数g(x)单调递增;当x∈$(-\frac{2}{3},1)$时,g′(x)<0,此时函数g(x)单调递减;当x∈(1,2]时,g′(x)>0,此时函数g(x)单调递增.
g(-$\frac{2}{3}$)=$\frac{22}{27}$,g(2)=2,可得g(x)max=2.
∴3a2-a>2,
解得a>1或a$<-\frac{2}{3}$.
可得:a的取值范围是a>1或a$<-\frac{2}{3}$.
点评 本题考查了利用导数研究函数的单调性极值与最值、恒成立问题等价转化方法、不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
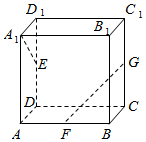 如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角的余弦值是0.
如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角的余弦值是0.