题目内容
方程2（k+1）x2+4kx+3k-2=0的一根比1大，一根比1小，则k的范围为 ．
考点：函数的零点与方程根的关系
专题：函数的性质及应用
分析：直接利用方程对应的二次函数零点的分布，推出关系式，求出a的范围即可．
解答：
解：由题意得：
或
，
解得：-1＜k＜0．
故答案为：（-1，0）．
|
|
解得：-1＜k＜0．
故答案为：（-1，0）．
点评：本题主要考查了一元二次方程的实根分布问题，解题的关键是熟练一元二次方程与二次函数的互化，属于基础题．
练习册系列答案
相关题目
若f（x）=2x，g（x）=log2x，则如上图所示的程序框图中，输入x=4，输出h（x）=（ ）
| A、16 | ||
B、
| ||
| C、2 | ||
D、
|
设复数z满足z•i=2015-i，i为虚数单位，则在复平面内，复数z对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
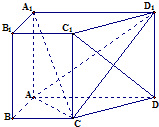如图，在直四棱柱ABCD-A1B1C1D1中，底面四边形ABCD是直角梯形，其中AB⊥AD，AB=BC=1且AD=设集合A={-1，0，1}，B={x∈R|x＞0}，则A∩B=（ ）
| A、{-1，0} | B、{-1} |
| C、{0，1} | D、{1} |