题目内容
17．已知实数x，y满足$\left\{\begin{array}{l}2x-y-4≤0\\ x-y+2≥0\\ x≥2\end{array}\right.$，则z=3x-y的最大值为10．分析 熟悉画出可行域，根据目标函数的几何意义求最大值即可．
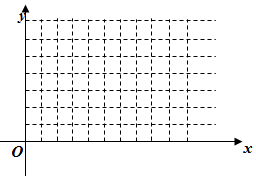
解答 解：由已知的不等式组得到平面区域如图
：
根据z=3x-y得到y=3x-z，
当此直线经过图中C时在y轴截距最小，z最大，
由$\left\{\begin{array}{l}{2x-y-4=0}\\{x-y+2=0}\end{array}\right.$得到C（6，8），
所以z的最大值为3×6-8=10；
故答案为：10．
点评 本题考查了简单线性规划问题；画出可行域，利用目标函数的几何意义求最值．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
5．
在一次抽样调查中测得样本的5个样本点，数值如表：
（1）作出散点图，并判断y与x之间是否具有相关关系．若y与x非线性关系，应选择下列哪个模型更合适？（y=$\frac{k}{x}$+b，y=k•lnx+b，y=eax+b）
（2）请利用前四组数据，试建立y与x之间的回归方程．（保留小数点后1位有效数字）
在一次抽样调查中测得样本的5个样本点，数值如表：| x | 0.25 | 0.5 | 1 | 2 | 4 |
| y | 16 | 12 | 5 | 2 | 1 |
（2）请利用前四组数据，试建立y与x之间的回归方程．（保留小数点后1位有效数字）
12．过点P（-2，0）的双曲线C与椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的焦点相同，则双曲线C的渐近线方程是（ ）
| A． | $y=±\frac{{\sqrt{3}}}{3}x$ | B． | $y=±\sqrt{3}x$ | C． | $y=±\frac{1}{2}x$ | D． | y=±2x |
2．设函数f（x）=sin（2x+$\frac{π}{3}$），则下列结论正确的是（ ）
| A． | f（x）的图象关于直线x=$\frac{π}{3}$对称 | |
| B． | f（x）的图象关于点（$\frac{π}{4}$，0）对称 | |
| C． | 把f（x）的图象向左平移$\frac{π}{12}$个单位长度，得到一个偶函数的图象 | |
| D． | f（x）的最小正周期为π，且在[0，$\frac{π}{6}$]上为增函数 |
已知三棱锥S-ABC，底面△ABC为边长为2的正三角形，侧棱SA=SC=$\sqrt{2}$，SB=2