题目内容
已知曲线C上动点P(x,y)到定点F1(
,0)与定直线l1:x=
的距离之比为常数
.
(1)求曲线C的轨迹方程;
(2)以曲线c的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与曲线C交于点M与点N,求
•
的最小值,并求此时圆T的方程.
| 3 |
4
| ||
| 3 |
| ||
| 2 |
(1)求曲线C的轨迹方程;
(2)以曲线c的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与曲线C交于点M与点N,求
| TM |
| TN |
分析:(1)利用条件,建立方程,化简,即可求曲线c的轨迹方程;
(2)用坐标表示出向量的数量积,再用配方法求最值,求出M的坐标,代入圆的方程,即可求得结论.
(2)用坐标表示出向量的数量积,再用配方法求最值,求出M的坐标,代入圆的方程,即可求得结论.
解答:解:(1)因为曲线C上动点P(x,y)到定点F1(
,0)与定直线l1:x=
的距离之比为常数
所以
=
,
所以椭圆的标准方程为
+y2=1.
(2)点M与点N关于x轴对称,设M(x1,y1),N(x2,y2),不妨设y1>0.
由于点M在椭圆C上,所以y12=1-
.
由已知T(-2,0),则
=(x1+2,y1),
=(x1+2,-y1),
∴
•
=(x1+2,y1)•(x1+2,-y1)=
(x1+
)2-
.
由于-2<x1<2,故当x1=-
时,
•
取得最小值为-
.
此时,y1=
,故M(-
,
),
又点M在圆T上,代入圆的方程得到r2=
.
故圆T的方程为:(x+2)2+y2=
.
| 3 |
4
| ||
| 3 |
| ||
| 2 |
所以
| ||||
|x-
|
| ||
| 2 |
所以椭圆的标准方程为
| x2 |
| 4 |
(2)点M与点N关于x轴对称,设M(x1,y1),N(x2,y2),不妨设y1>0.
由于点M在椭圆C上,所以y12=1-
| x12 |
| 4 |
由已知T(-2,0),则
| TM |
| TN |
∴
| TM |
| TN |
| 5 |
| 4 |
| 8 |
| 5 |
| 1 |
| 5 |
由于-2<x1<2,故当x1=-
| 8 |
| 5 |
| TM |
| TN |
| 1 |
| 5 |
此时,y1=
| 3 |
| 5 |
| 8 |
| 5 |
| 3 |
| 5 |
又点M在圆T上,代入圆的方程得到r2=
| 13 |
| 25 |
故圆T的方程为:(x+2)2+y2=
| 13 |
| 25 |
点评:本题考查椭圆的标准方程,考查向量的数量积公式,考查配方法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
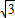 ,0)与定直线l1:x=
,0)与定直线l1:x=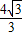 的距离之比为常数
的距离之比为常数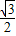 .
. •
• 的最小值,并求此时圆T的方程.
的最小值,并求此时圆T的方程. ,0)与定直线l1:x=
,0)与定直线l1:x= 的距离之比为常数
的距离之比为常数 .
. )引曲线C的弦AB恰好被点Q平分,求弦AB所在的直线方程;
)引曲线C的弦AB恰好被点Q平分,求弦AB所在的直线方程; 的最小值,并求此时圆T的方程.
的最小值,并求此时圆T的方程.