题目内容
设正整数数列{an}满足:a1=2,a2=6,当n≥2时,有|a2n-an-1an+1|<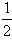 an-1。
an-1。
(1)求a3、a4的值;
(2)求数列{an}的通项公式;
(3)记Tn=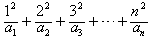 ,证明:对任意的n∈N*,都有Tn<
,证明:对任意的n∈N*,都有Tn<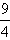 。
。
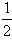 an-1。
an-1。(1)求a3、a4的值;
(2)求数列{an}的通项公式;
(3)记Tn=
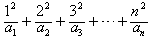 ,证明:对任意的n∈N*,都有Tn<
,证明:对任意的n∈N*,都有Tn<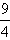 。
。解:(1)n=2时,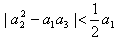
由已知a1=2,a2=6,得|36-2a3|<1,
因为a3为正整数,
所以a3=18,同理a4=54。
(2)由(1)可猜想:an=2·3n-1,(*)
给出证明:①n=1,2时(*)式成立;
②假设当n=k-1与n=k时(*)式成立,即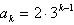
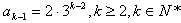
于是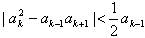
整理得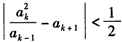
于是得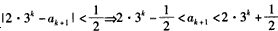
因为ak+1为正整数,
所以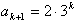
即当n=k+1时(*)式仍成立
综上所述,对于任意的n∈N*,有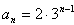 成立
成立
故数列{an}的通项公式为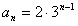 。
。
(3)由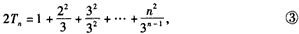
得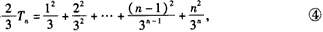
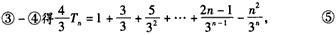
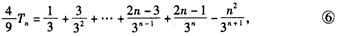
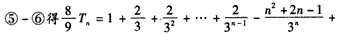
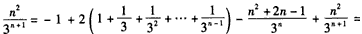
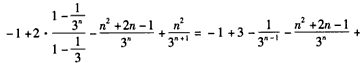
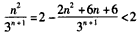
故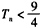 。
。
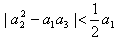
由已知a1=2,a2=6,得|36-2a3|<1,
因为a3为正整数,
所以a3=18,同理a4=54。
(2)由(1)可猜想:an=2·3n-1,(*)
给出证明:①n=1,2时(*)式成立;
②假设当n=k-1与n=k时(*)式成立,即
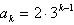
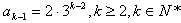
于是
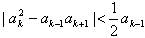
整理得
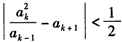
于是得
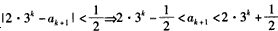
因为ak+1为正整数,
所以
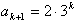
即当n=k+1时(*)式仍成立
综上所述,对于任意的n∈N*,有
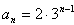 成立
成立故数列{an}的通项公式为
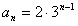 。
。(3)由
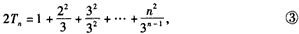
得
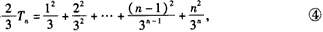
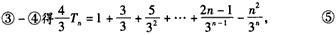
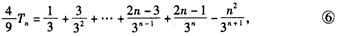
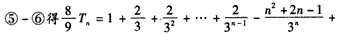
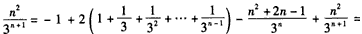
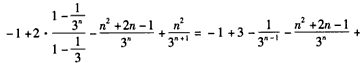
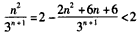
故
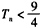 。
。
练习册系列答案
相关题目
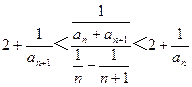 .
.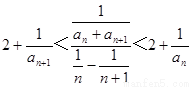 .
.