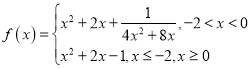题目内容
【题目】已知抛物线![]() ,焦点为
,焦点为![]() ,直线
,直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,
两点,![]() 是线段
是线段![]() 的中点,过
的中点,过![]() 作
作![]() 轴的垂线交抛物线
轴的垂线交抛物线![]() 于点
于点![]() .
.
(1)求抛物线![]() 的焦点坐标;
的焦点坐标;
(2)若抛物线![]() 上有一点
上有一点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() ,求此时
,求此时![]() 的值;
的值;
(3)是否存在实数![]() ,使
,使![]() 是以
是以![]() 为直角顶点的直角三角形?若存在,求出
为直角顶点的直角三角形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,2.
;(3)存在,2.
【解析】
(1)抛物线![]() ,即
,即![]() ,可求出焦点坐标,即可求得答案;
,可求出焦点坐标,即可求得答案;
(2)利用抛物线的定义把焦点![]() 的距离为
的距离为![]() 转化为到准线的距离为
转化为到准线的距离为![]() ,即可求得答案;
,即可求得答案;
(3)![]() 是以
是以![]() 为直角顶点的直角三角形即是
为直角顶点的直角三角形即是![]() ,把直线方程和抛物线方程联立,可以得到
,把直线方程和抛物线方程联立,可以得到![]() 两点的坐标进而求得
两点的坐标进而求得![]() 以及
以及![]() 的坐标,代入是
的坐标,代入是![]() ,即可求得答案.
,即可求得答案.
(1)抛物线![]() ,
,
即![]()
∴抛物线![]() 的焦点为
的焦点为![]()
(2)∵抛物线![]() 上有一点
上有一点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() ,
,
![]()
![]()
(3)联立方程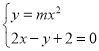 消去
消去![]()
可得![]() ,
,
设![]()
则![]()
![]() ①
①
![]()
![]() 是线段
是线段![]() 的中点,
的中点,
![]()
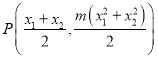 ,即
,即![]()
![]()
得![]()
若存在实数![]() ,使
,使![]() 是以
是以![]() 为直角顶点的直角三角形,则是
为直角顶点的直角三角形,则是![]()
即![]()
结合①化简得![]()
即![]()
![]() 或
或![]() (舍去),经检验满足判别式大于0
(舍去),经检验满足判别式大于0
![]() 存在实数
存在实数![]() ,使
,使![]() 是以
是以![]() 为直角顶点的直角三角形.
为直角顶点的直角三角形.

练习册系列答案
相关题目
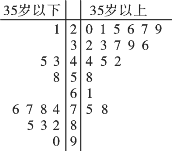
【题目】某单位对其![]() 名员工的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于
名员工的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于![]() 的人,喜食蔬菜;饮食指数高于
的人,喜食蔬菜;饮食指数高于![]() 的人,喜食肉类).
的人,喜食肉类).
(1)根据所给数据完成下面的![]() 列联表;
列联表;
喜食蔬菜 | 喜食肉类 | 总计 | |
35岁以上 | |||
35岁以下 | |||
总计 |
(2)能否有![]() 的把握认为该单位员工的饮食习惯与年龄有关?
的把握认为该单位员工的饮食习惯与年龄有关?
独立性检验的临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: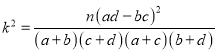 ,
,![]() .
.