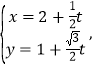题目内容
【题目】已知抛物线![]() :
:![]() 上一点
上一点![]() 到其准线的距离为2.
到其准线的距离为2.

(1)求抛物线![]() 的方程;
的方程;
(2)如图![]() ,
,![]() ,
,![]() 为抛物线
为抛物线![]() 上三个点,
上三个点,![]() ,若四边形
,若四边形![]() 为菱形,求四边形
为菱形,求四边形![]() 的面积.
的面积.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]()
【解析】
(1)利用点在抛物线上和焦半径公式列出关于![]() 的方程组求解即可。
的方程组求解即可。
(2)设出A,C点的坐标及直线AC,利用设而不求和韦达定理求出AC中点的坐标,然后求出B点的坐标,利用B在抛物线上以及直线BD和直线AC的斜率互为负倒数列出方程组求出B点坐标,然后求出AC的长度,即可求出面积。
(1)由已知可得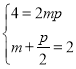 ,
,
消去![]() 得:
得:![]() ,
,![]()
抛物线![]() 的方程为
的方程为![]()
(2)设![]() ,
,![]() ,菱形
,菱形![]() 的中心
的中心![]()
当![]() 轴,则
轴,则![]() 在原点,
在原点,![]() ,
,
![]() ,
,![]() ,菱形的面积
,菱形的面积![]() ,
,
解法一:当![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 方程:
方程:![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]()
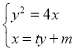 消去
消去![]() 得:
得:![]()

![]()
![]() ,
,![]() ,∵
,∵![]() 为
为![]() 的中点
的中点
∴![]() ,点
,点![]() 在抛物线上,
在抛物线上,
且直线![]() 的斜率为
的斜率为![]() 。
。
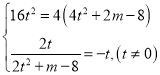 解得:
解得:![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
综上,![]() 或
或![]()
解法二:设![]() ,直线
,直线![]() 的斜率为
的斜率为![]()
![]()
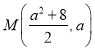 ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
可以设直线![]() :
:![]()
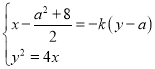 消去
消去![]() 得:
得:![]()
∵![]()
![]() ,
,![]()
解方程:![]() ,解得
,解得![]() ,
,![]() ,接下去同上。
,接下去同上。

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目