题目内容
14．
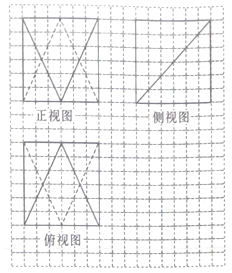如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某个多面体的三视图，则该多面体的体积为（ ）| A． | 72 | B． | $90\sqrt{3}$ | C． | $108\sqrt{2}$ | D． | 144 |
分析 该几何体是一个八面体，它由两个共底面的四棱锥构成．画出直观图，计算可得答案．
解答 解：该几何体是一个八面体，它由两个共底面的四棱锥构成．
它也可看成一个边长为5的立方体去掉四个全等的直角三棱锥（三条直角边长为6，6，3）得到（如下图）．
解法1：$V=\frac{1}{3}×6×6\sqrt{2}×6\sqrt{2}=144$．
解法2：$V={6^3}-4×\frac{1}{6}×6×6×3=144$．
故选D．
点评 本题考查的知识点是棱柱的体积和表面积，棱锥的体积和表面积，简单几何体的三视图，难度中档．
练习册系列答案
阅读快车系列答案
相关题目
9．三棱锥B-ACD的每个顶点都在表面积为16π的球O的球面上，且AB⊥平面BCD，△BCD为等边三角形，AB=2BC，则三棱锥B-ACD的体积为（ ）
| A． | 3 | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{3}{2}$ | D． | $\sqrt{3}$ |
19．若函数f（x）=g（x）+x2为奇函数，且f（1）=1，则函数g（x）的解析式可能为（ ）
| A． | y=x3 | B． | y=2x3-x2 | C． | y=2x3+x2 | D． | y=x5-x2 |
6．设{an}是等比数列，且a1=$\frac{3}{2}$，S3=$\frac{9}{2}$，则它的通项公式为an=（ ）
| A． | $\frac{3}{2}$•（$\frac{1}{2}$）n-1 | B． | $\frac{3}{2}•{（{-\frac{1}{2}}）^{n-2}}$ | C． | $\frac{3}{2}$•（-$\frac{1}{2}$）n-2 | D． | $\frac{3}{2}$•（-2）n-1或$\frac{3}{2}$ |
3．设a＞1，函数f（x）=loga（a2x-2ax-2），则使f（x）＞0的x的取值范围是（ ）
| A． | （-∞，0） | B． | （-∞，loga3） | C． | （0，+∞） | D． | （loga3，+∞） |
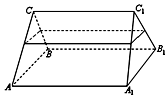如图，一个三棱柱形容器中盛有水，且侧棱AA1=8．若侧面AA1B1B水平放置时，液面恰好过AC，BC，A1C1，B1C1的中点．则当底面ABC水平放置时，液面高为（ ）