题目内容
11.已知(ax+b)6的展开式中x4项的系数与x5项的系数分别为135与-18,则(ax+b)6展开式所有项系数之和为( )| A. | -1 | B. | 1 | C. | 32 | D. | 64 |
分析 由题意先求得a、b的值,再令x=1求出展开式中所有项的系数和.
解答 解:(ax+b)6的展开式中x4项的系数与x5项的系数分别为135与-18,
∴${C}_{6}^{4}$•a4•b2=135①,
${C}_{6}^{5}$•a5•b=-18②;
由①、②组成方程组$\left\{\begin{array}{l}{1{{5a}^{4}b}^{2}=135}\\{{6a}^{5}b=-18}\end{array}\right.$,
解得a=1,b=-3或a=-1、b=3;
∴令x=1,求得(ax+b)6展开式中所有项系数之和为26=64.
故选:D.
点评 本题考查了二项式定理的应用问题,求出系数a、b是解题的关键,属基础题.

练习册系列答案
相关题目
1.已知一个圆锥的正视图和侧视图都是边长为1的正三角形,则它的俯视图的面积是( )
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
2.执行如图所示的程序框图,则输出的a值为( )
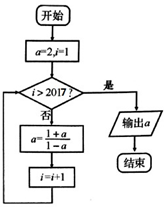

| A. | -3 | B. | $\frac{1}{3}$ | C. | $-\frac{1}{2}$ | D. | 2 |
19.以(1,0),(-1,0)为焦点的椭圆与y=x-2有公共点,则该椭圆离心率的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
6.已知复数$z=\frac{2+i}{1-i}$(i为虚数单位),那么z的共轭复数为( )
| A. | $\frac{3}{2}+\frac{3}{2}i$ | B. | $\frac{1}{2}-\frac{3}{2}i$ | C. | $\frac{1}{2}+\frac{3}{2}i$ | D. | $\frac{3}{2}-\frac{3}{2}i$ |
3.已知集合S={0,1,2,3,4,5,6},T={x|x2-6x+5≤0},则S∩T=( )
| A. | {2,3,4} | B. | {1,2,3,4,5} | C. | {2,3} | D. | T |